Призма. Формулы и свойства призмы
Навигация по странице:
Определение призмы
Элементы призмы
Прямая призма
Наклонная призма
Правильная призма
Усечённая призма
Объём призмы
Площадь поверхности призмы
Основные свойства призмы
Определение.
Призма — это многогранная объемная фигура, которая состоит из двух одинаковых плоских многоугольников (основ), находящихся в двух параллельных плоскостях, а другие грани (боковые грани) - параллелограммы, что имеют общие стороны с этими многоугольниками.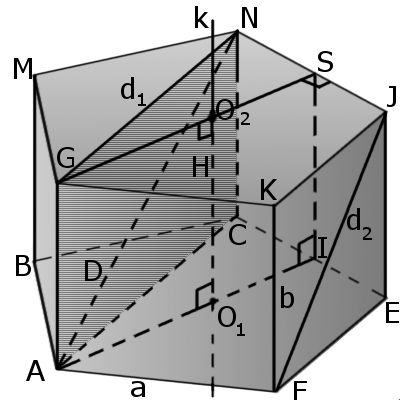 |
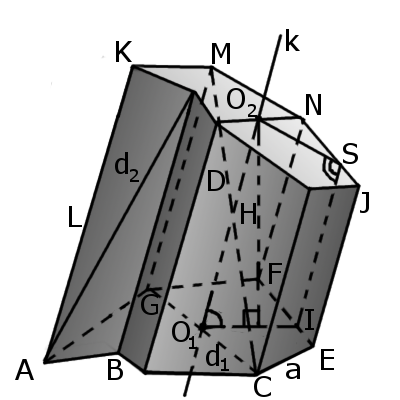 |
|
| Рис.1 | Рис.2 |
Определение. Основы призмы - две грани, которые являются равными параллельными плоскими многоугольниками (ABCEF, GMNJK).
Определение. Боковые грани призмы - все остальные грани за исключением основ.
Определение. Боковая поверхность призмы - совокупность всех боковых граней призмы.
Определение. Поверхность призмы - это совокупность поверхностей двух оснований и боковой поверхности.
Определение. Боковое ребро призмы - общая сторона двух боковых граней.
Определение. Высота - это перпендикуляр, который соединяет две основы призмы под прямым углом.
Определение. Диагональ основания призмы - это отрезок, соединяющий две не соседние вершины, принадлежащие этой же основе.
Определение. Диагональ боковой грани призмы - это отрезок, соединяющий две противоположные вершины, лежащие на одной боковой грани однако принадлежат различным основам.
Определение. Диагональ призмы (AN) - это отрезок, соединяющий две вершины, лежащие на разных основаниях, но не лежат на одной боковой стороне.
Определение. Диагональное сечение - это пересечение призмы плоскостью, проходящей через диагональ основания призмы и боковое ребро. Треугольная призма (в основе призмы треугольники) не имеет диагональных сечений.
Определение. Перпендикулярное сечение - это пересечение призмы плоскостью, пересекающей боковые ребра призмы под прямым углом.
Определение. Прямая призма - это призма, в которой все боковые грани перпендикулярны к основанию. Высота равна длине бокового ребра.
Определение. Наклонная призма - это призма, в которой боковые грани не перпендикулярны к основанию.
Определение. Правильная призма - это призма, в которой основы являются правильными многоугольниками. Правильная призма может быть, как прямой, так и наклонной.
Определение. Усечённая призма - это призма, в которой две основы не параллельны (рис. 2). Усечённая призма может быть, как прямой, так наклонной.
Объём призмы
Формула. Объём призмы через площадь основания и высоту:
V = SоснH
Формула. Объём наклонной призмы через площадь перпендикулярного сечения и длину бокового ребра:
V = SпL
Формула.
Объём правильной прямой призмы через высоту (h), длину стороны (a) и количество сторон (n):
| V = | n | ha2ctg | π |
| 4 | n |
Площадь поверхности призмы
Формула. Площадь боковой поверхности призмы через периметр основания и высоту:
Sb = P·h
Формула. Площадь поверхности призмы через площадь основания, периметр основания и высоту:
S = 2Soсн + P·h
Формула.
Площадь поверхности правильной призмы через высоту (h), длину стороны (a) и количество сторон (n):
| S = | n | a2ctg | π | + nah |
| 2 | n |
Основные свойства призмы
Основы призмы - равные многоугольники.
Боковые грани призмы - параллелограммы.
Боковые ребра призмы параллельны и равны между собой.
Перпендикулярное сечение перпендикулярно всем боковым ребрам и боковым граням.
Высота прямой призмы равна длине бокового ребра.
Высота наклонной призмы всегда меньше длины ребра.
В прямой призме гранями могут быть прямоугольниками или квадратами.
Формулы по геометрии
Треугольник. Формулы и свойства треугольника  Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
 Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
