Окружность, круг, сегмент, сектор. Формулы и свойства
- Окружность - определение
- Круг - определение
- Радиус и диаметр окружности
- Основные свойства окружности
- Формулы длины окружности и площади круга
- Уравнение окружности
- Касательная окружности и ее свойства
- Секущая окружности и ее свойства
- Хорда окружности и ее свойства
- Центральный угол, вписанный угол и их свойства
- Дуга, длина дуги, градусная мера дуги
- Полуокружность и полукруг
- Сектор, площадь сектора
- Сегмент, площадь сегмента
- Концентрические окружности
- Кольцо
 |
 |
 |
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность - окружность, радиус которой равен единице.
Определение. Круг - часть плоскости, ограничена окружностью.
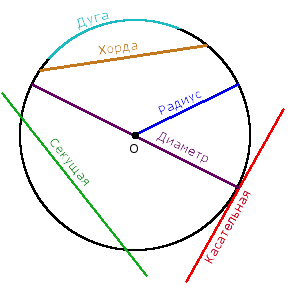
Определение. Радиус окружности R - расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D - отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S =
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x - a)2 + (y - b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности - прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
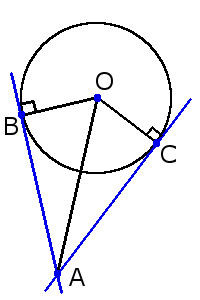
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности - прямая, которая проходит через две точки окружности.
Основные свойства секущих

AQ ∙ BQ = CQ ∙ DQ

AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности - отрезок, который соединяет две точки окружности.
Длина хорды

AB = 2r sin

AB = 2r sin α
Основные свойства хорд

если хорды AB = CD, то
дуги ◡ AB = ◡ CD
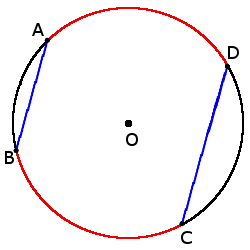
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
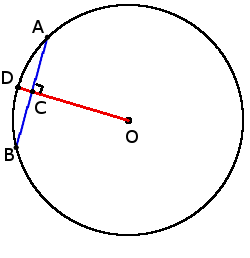
если OD ┴ AB, то
AC = BC
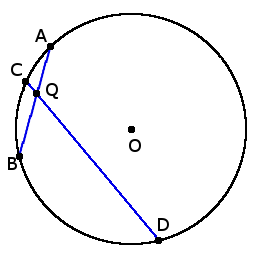
AQ ∙ BQ = DQ ∙ QC
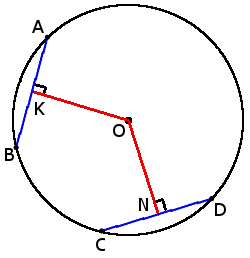
если хорды AB = CD, то
ON = OK
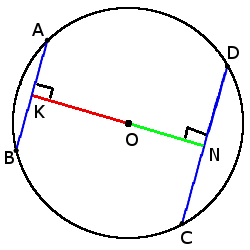
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
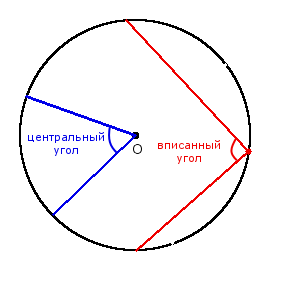
Определение. Центральный угол окружности - угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность - угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
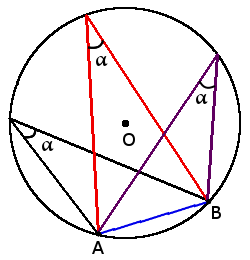
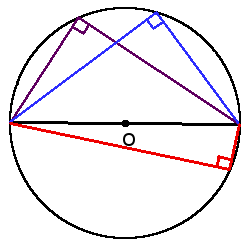

β =

α + β = 180°
Определение. Дуга окружности (◡) - часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги - угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
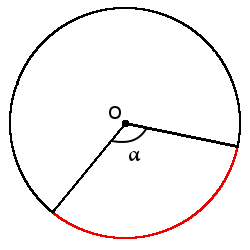
l =
Определение. Полуокружность - дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) - часть круга, которая ограничена полуокружностью и диаметром.
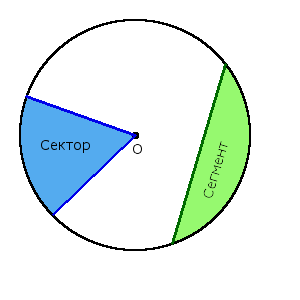
Определение. Сектор (◔) - часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

S =
Определение. Сегмент - часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности - окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо - часть плоскости ограниченная двумя концентрическими окружностями.
Формулы по геометрии
Треугольник. Формулы и свойства треугольника  Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
 Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
