Куб. Формулы, признаки и свойства куба

Навигация по странице: Определение куба Грань куба Ребро куба Вершина куба Центр грани куба Центр куба Ось куба Диагональ куба Диагональ грани куба Объём куба Площадь поверхности куба Периметр куба Сфера вписана в куб Сфера описана вокруг куба Свойства куба Координати вершин куба Единичный куб Пересечение единичного куба плоскостью

Определение.

Куб (гексаедр) — это трехмерная фигура, которая состоит из шести динаковых квадратов так, что каждый квадрат полностью соприкасается своими четырьмя сторонами к сторонам остальных четырех квадратов под прямым углом. Куб является правильным многогранником, у которого грани образованы из квадратов. Также кубом можно назвать прямоугольный параллелепипед, у которого все ребра равны.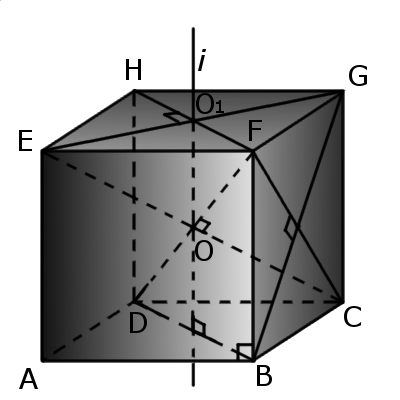

Определение. Грань куба - это часть плоскости, ограниченная сторонами квадрата.

- куб имеет шесть граней;

- каждая грань куба пересекается с четырьмя другими гранями под прямым углом и параллельная шестой грани;

- грани имеют одинаковую площадь, которую можно найти, используя формулы для вычисления площади квадрата.

Определение. Ребро куба - это отрезок, образованный пересечением двух граней куба.

- куб имеет двенадцать ребер;

- каждый конец ребра соединен с двумя соседними ребрами под прямым углом;

- ребра куба имеют одинаковую длину.

Определение. Вершина куба - это самая отдаленная от центра куба точка, которая лежит на пересечения трех граней куба.

- куб имеет восемь вершин;

- каждая вершина образована только тремя гранями и тремя ребрами.

Определение. Центр грани куба (O₁) - это равноудалена точка от всех ребер грани куба.

Определение. Центр куба (O) - это равноудалена точка от всех граней куба.

Определение. Ось куба (i) - это прямая, проходящая через центр куба и центры двух параллельных граней куба.

- куб имеет три оси;

- оси куба взаимно перпендикулярны.

Определение. Диагональ куба (d₁) - отрезок, который соединяет противоположные вершины куба и проходит через центр куба.

- куб имеет четыре диагонали;

- диагонали куба пересекаются и делятся пополам в центре куба;

- диагонали куба имеют одинаковую длину.

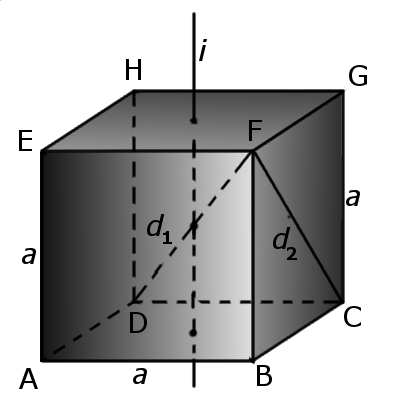
Формула. Диагональ куба d₁ через длину ребра a:

d₁ = a√3

Определение. Диагональ грани куба (d₂) -отрезок, который соединяет противоположные углы грани куба и проходит через центр грани куба.

Формула. Диагональ грани d₂ через длину ребра a:

d₂ = a√2

Определение. Объём куба - это совокупность всех точек в пространстве, ограниченные гранями куба.

Формула. Объём куба через длину ребра a:

V = a³

Формула. Объём куба через длину диагонали куба d₁:

V =	d₁³
	3√3

Определение. Площадь поверхности куба - это совокупность плоскостей всех граней.

Формула. Площадь поверхности куба через длину ребра a:

S = 6a²

Определение. Периметр куба - это совокупность длин всех ребер куба.

Формула. Периметр куба P через длину ребра a:

P = 12a

Определение. Сферой вписанной в куб называется сфера, центр которой совпадает с центром куба и которая касается центров граней куба.

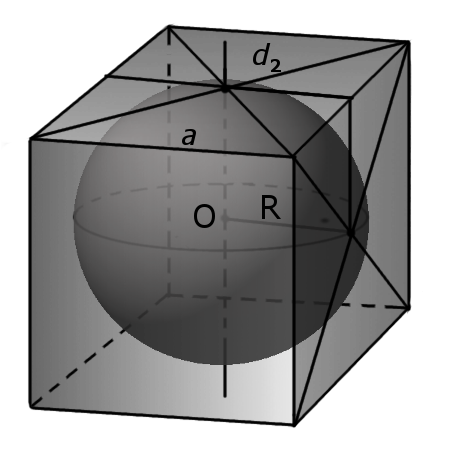
- все шесть граней куба являются касательными плоскостями к вписанной сферы;

- радиус вписанной сферы равен половине длины ребра a.

Формула. Радиус вписанной сферы r через длину ребра a:

r =	a
	2

Формула. Объема вписанной сферы V через длину ребра a:

V =	π a³
	6

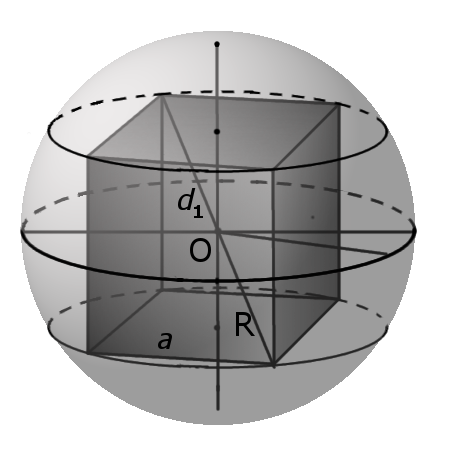
Сфера описана вокруг куба с обозначениями

Определение. Сферой описанной вокруг куба называется сфера, центр которой совпадает с центром куба и которая соприкасается с восьмью вершинами куба.

- радиус описанной сферы равен половине длины диагонали (d₁) куба.

Формула. Радиус описанной сферы R через длину ребра a:

R =	a√3
	2

Формула. Объема сферы описанной вокруг куба V через длину ребра a:

V =	π a³√3
	2

Свойства куба

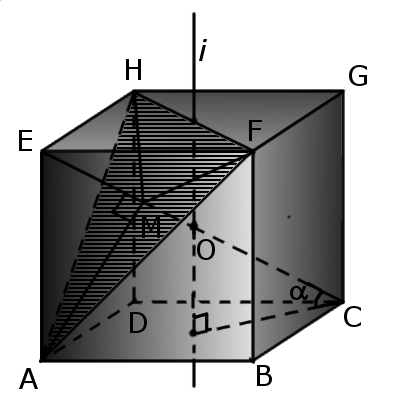
1. В куб можно вписать тетраэдр так, чтобы все четыре вершины тетраэдра лежали на четырех вершинах куба, а все шесть ребер тетраэдра будут лежать на шести гранях куба и ребра будут равны диагонали грани куба.

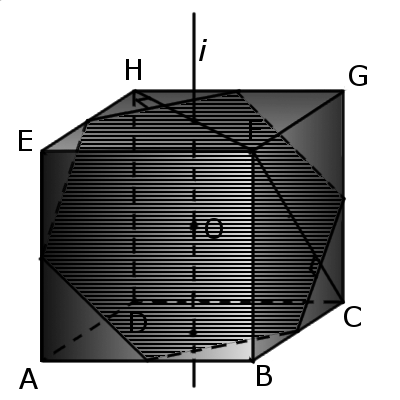
2. В куб можно вписать правильный шестиугольник так, что все шесть вершин лежат в центрах граней куба.

Координаты вершин куба

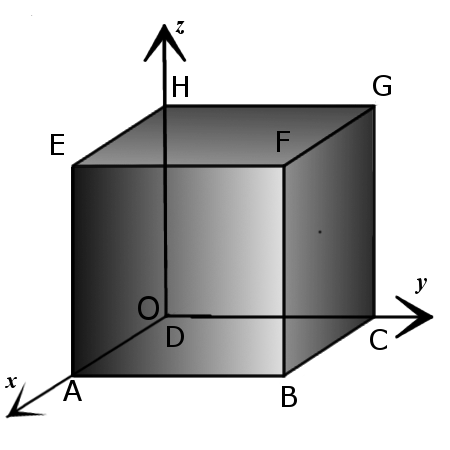
1. Координаты вершин куба со стороной a и вершиной D в начале декартовой системы координат так, что ребра этой вершины лежат на осях координат:

A(a, 0, 0), B(a, a, 0), C(0, a, 0), D(0, 0, 0),
E(a, 0, a), F(a, a, a), G(0, a, a), H(0, 0, a).

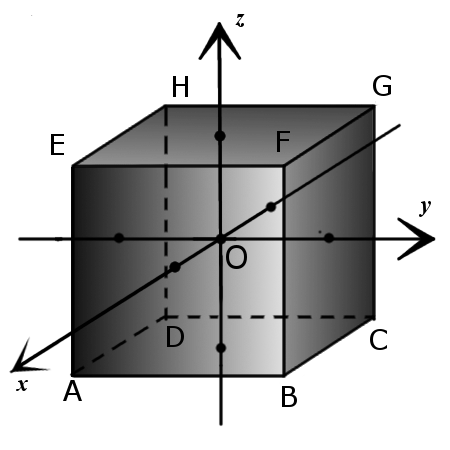
2. Координаты вершин куба с длиной стороны 2a, у которого центр куба находится в начале декартовой системы координат так, что ребра куба параллельны осям координат:

A(a, -a, -a), B(a, a, -a), C(-a, a, -a), D(-a, -a, -a),
E(a, -a, a), F(a, a, a), G(-a, a, a), H(-a, -a, a).

Определение. Единичный куб - это куб, у которого длина ребер равна единице.

Пересечение куба плоскостью

1. Если пересечь куб плоскостью, проходящей через центр куба и центры двух противоположных граней, то в сечении будет квадрат, длина стороны которого будет равна длине ребра куба. Эта плоскость делит куб два равных прямоугольных параллелепипеда.

2. Если пересечь куб с ребром a плоскостью, проходящей через центр куба и два параллельных ребра, то в сечении будет прямоугольник со сторонами a и a√2, площадью сечения a²√2. Эта плоскость делит куб две равные призмы.

3. Если пересечь куб плоскостью, проходящей через центр и середины шести граней, то в сечении будет правильный шестиугольник со стороной a√2/2, площадью сечения a²(3√3)/4. У куба одна из диагоналей (FC) каждой грани, что пересекаются, перпендикулярна стороне шестиугольника.

4. Если пересечь куб плоскостью, проходящей через три вершины куба, то в сечении будет правильный треугольник со стороной a√2, площадью сечения a²√3/2 и объемом большей части - 5a³/6 и меньшей - a³/6. Одна из диагоналей куба (EC) перпендикулярна к плоскости сечения и проходит через центр треугольника (M) и делится плоскостью в отношении MC:EМ = 2:1.

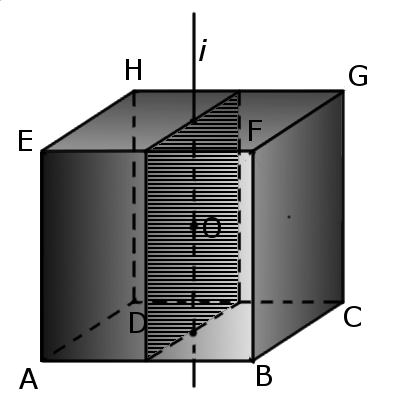
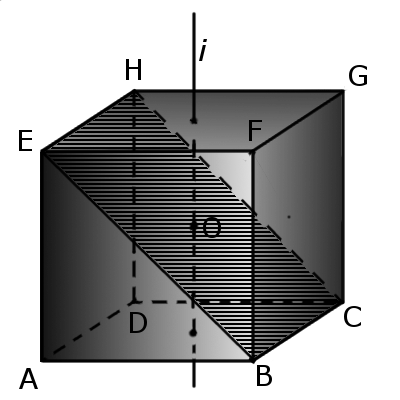
Формулы по геометрии Треугольник. Формулы и свойства треугольника