Ромб. Формулы, признаки и свойства ромба
Навигация по странице:
Определение ромба
Признаки ромба
Основные свойства ромба
Стороны ромба
Диагонали ромба
Периметр ромба
Площадь ромба
Окружность вписанная в ромб
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.Ромбы отличаются между собой размером стороны и размером углов.
 |
 |
|
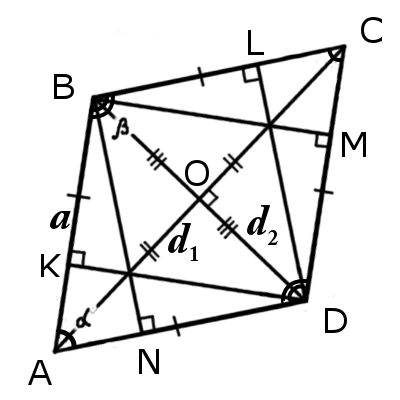
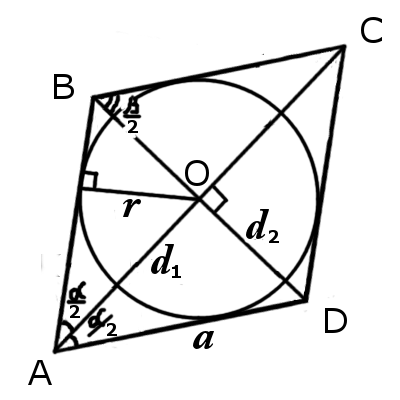
| Рис.1 | Рис.2 |
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
1. Имеет все свойства параллелограмма
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √S |
| √sinα |
| a = | √S |
| √sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2r |
4. Формула стороны ромба через две диагонали:
| a = | √d12 + d22 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
| a = | d1 |
| √2 + 2 cosα |
| a = | d2 |
| √2 - 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d1 |
| 2cos(α/2) |
| a = | d1 |
| 2sin(β/2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d2 |
| 2cos(β/2) |
| a = | d2 |
| 2sin(α/2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.Ромб имеет две диагонали - длинную d1, и короткую - d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 - 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 - 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 - d22
d2 = √4a2 - d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
| d1 = | 2S |
| d2 |
| d2 = | 2S |
| d1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d1 = | 2r |
| sin(α/2) |
| d2 = | 2r |
| sin(β/2) |
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
| S = | 1 | d1d2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4r2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
| S = | 1 | d12 · tg(α/2) |
| 2 |
| S = | 1 | d22 · tg(β/2) |
| 2 |
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d1 · sin(α/2) |
| 2 |
| r = | d2 · sin(β/2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d1 · d2 |
| 2√d12 + d22 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d1 · d2 |
| 4a |
Формулы по геометрии
Треугольник. Формулы и свойства треугольника  Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
 Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
