Трапеция. Формулы, признаки и свойства трапеции

Навигация по странице: Определение трапеции Элементы трапеции Виды трапеций Основные свойства трапеции Стороны трапеции Средняя линия трапеции Высота трапеции Диагонали трапеции Площадь трапеции Периметр трапеции Окружность описанная вокруг трапеции Окружность вписанная в трапецию Другие отрезки трапеции

Определение.

Трапеция — это четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.

Параллельные стороны называются основами трапеции, а две другие боковыми сторонами

Так же, трапецией называется четырехугольник, у которого одна пара противоположных сторон параллельна, и стороны не равны между собой.

Элементы трапеции:

Основы трапеции - параллельные стороны
Боковые стороны - две другие стороны
Средняя линия - отрезок, соединяющий середины боковых сторон.

Виды трапеций:

Равнобедренная трапеция - трапеция, у которой боковые стороны равны
Прямоугольная трапеция - трапеция, у которой одна из боковых сторон перпендикулярна основам


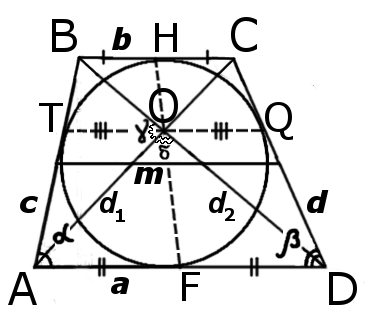
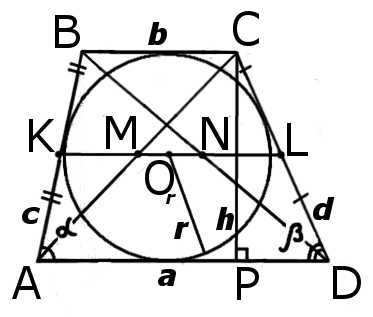
Рис.1		Рис.2

Основные свойства трапеции

1. В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

AB + CD = BC + AD

2. Средняя линия трапеции разделяет пополам любой отрезок, который соединяет основы, так же делит диагонали пополам:

AK = KB, AM = MC, BN = ND, CL = LD

3. Средняя линия трапеции параллельна основаниям и равна их полусумме:

m =	a + b
	2

4. Точка пересечения диагоналей трапеции и середины оснований лежат на одной прямой.

5. В трапеции её боковая сторона видна из центра вписанной окружности под углом 90°.

6. Каждая диагональ в точке пересечения делится на две части с таким соотношением длины, как соотношение между основаниями:

BC : AD = OC : AO = OB : DO

7. Диагонали трапеции d₁ и d₂ связаны со сторонами соотношением:

d₁² + d₂² = 2ab + c² + d²

Сторона трапеции

Формулы определения длин сторон трапеции:

1. Формула длины оснований трапеции через среднюю линию и другую основу:

a = 2m - b

b = 2m - a

2. Формулы длины основ через высоту и углы при нижнем основании:

a = b + h · (ctg α + ctg β)

b = a - h · (ctg α + ctg β)

3. Формулы длины основ через боковые стороны и углы при нижнем основании:

a = b + c·cos α + d·cos β

b = a - c·cos α - d·cos β

4. Формулы боковых сторон через высоту и углы при нижнем основании:

с =	h	d =	h
	sin α		sin β

Средняя линия трапеции

Определение.

Средняя линия - отрезок, соединяющий середины боковых сторон трапеции.

Формулы определения длины средней линии трапеции:

1. Формула определения длины средней линии через длины оснований:

m =	a + b
	2

2. Формула определения длины средней линии через площадь и высоту:

m =	S
	h

Высота трапеции

Формулы определения длины высоты трапеции:

1. Формула высоты через сторону и прилегающий угол при основании:

h = c·sin α = d·sin β

2. Формула высоты через диагонали и углы между ними:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
		a + b			a + b

3. Формула высоты через диагонали, углы между ними и среднюю линию:

h =	sin γ ·	d₁ d₂	=	sin δ ·	d₁ d₂
		2m			2m

4. Формула высоты трапеции через площадь и длины оснований:

h =	2S
	a + b

5. Формула высоты трапеции через площадь и длину средней линии:

h =	S
	m

Диагонали трапеции

Формулы определения длины диагоналей трапеции:

1. Формулы диагоналей по теореме косинусов:

d₁ = √a² + d² - 2ad·cos β

d₂ = √a² + c² - 2ac·cos α

2. Формулы диагоналей через четыре стороны:

d₁ =	√	d ² + ab -	a(d ² - c²)
			a - b

d₂ =	√	c² + ab -	a(c² - d ²)
			a - b

3. Формула длины диагоналей через высоту:

d₁ = √h² + (a - h · ctg β)² = √h² + (b + h · ctg α)²

d₂ = √h² + (a - h · ctg α)² = √h² + (b + h · ctg β)²

4. Формулы длины диагонали через сумму квадратов диагоналей:

d₁ = √c² + d ² + 2ab - d₂²

d₂ = √c² + d ² + 2ab - d₁²

Площадь трапеции

Формулы определения площади трапеции:

1. Формула площади через основания и высоту:

S =	(a + b)	· h
	2

2. Формула площади через среднюю линию и высоту:

S = m · h

3. Формула площади через диагонали и угол между ними:

S =	d₁d₂	· sin γ	=	d₁d₂	· sin δ
	2			2

4. Формула площади через четыре стороны:

S =	a + b	√	c² -	(	(a - b)² + c² - d ²	)	²
	2				2(a - b)

5. Формула Герона для трапеции

S =	a + b	√(p - a)(p - b)(p - a - c)(p - a - d)
	\|a - b\|

где

p =	a + b + c + d	- полупериметр трапеции.
	2

Периметр трапеции

Формула определения периметра трапеции:

1. Формула периметра через основания:

P = a + b + c + d

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
	4√p(p - a)(p - c)(p - d₁)

где

p =	a + c + d₁
	2

a - большее основание

Окружность вписанная в трапецию

В трапецию можно вписать окружность, если сумма длин оснований равна сумме длин боковых сторон:

a + b = c + d

Формула определения радиуса вписанной в трапецию окружности

1. Формула радиуса вписанной окружности через высоту:

r =	h
	2

Другие отрезки разносторонней трапеции

Формулы определения длин отрезков проходящих через трапецию:

1. Формула определения длин отрезков проходящих через трапецию:

KM = NL =	b	KN = ML =	a	TO = OQ =	a · b
	2		2		a + b

Формулы по геометрии Треугольник. Формулы и свойства треугольника

Квадрат. Формулы и свойства квадрата

Прямоугольник. Формулы и свойства прямоугольника

Параллелограмм. Формулы и свойства параллелограмма

Ромб. Формулы и свойства ромба

Трапеция. Формулы и свойства трапеции

- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции

- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции

Правильный многоугольник. Формулы и свойства правильного многоугольника

Окружность, круг, сегмент, сектор. Формулы и свойства

Эллипс. Формулы и свойства эллипса

Куб. Формулы и свойства куба

Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда Призма. Формулы и свойства призмы

Пирамида. Формулы и свойства пирамиды

Сфера, шар, сегмент и сектор. Формулы и свойства

Цилиндр. Формулы и свойства

Конус. Формулы и свойства

Формулы площади геометрических фигур S Формулы периметра геометрических фигур P Формулы объема геометрических фигур V Формулы площади поверхности геометрических фигур S

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!