Направляющие косинусы вектора.
Навигация по странице:
Определение направляющих косинусов
Определение. Направляющие косинусы вектора a – это косинусы углов, которые вектор образует с положительными полуосями координат.
Направляющие косинусы однозначно задают направление вектора.
Основное соотношение. Чтобы найти направляющие косинусы вектора a необходимо соответствующие координаты вектора поделить на модуль вектора.
Соответственно, координаты единичного вектора равны его направляющим косинусам.
Свойство направляющих косинусов. Сумма квадратов направляющих косинусов равна единице.
Формулы вычисления направляющих косинусов вектора
Формула вычисления направляющих косинусов вектора для плоских задач
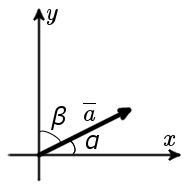
В случае плоской задачи (рис. 1) направляющие косинусы вектора a = {ax ; ay} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay |
| |a| | |a| |
Свойство:
cos2 α + cos2 β = 1
 |
| рис. 1 |
Формула вычисления направляющих косинусов вектора для пространственных задач
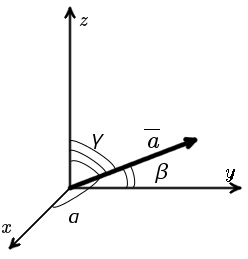
В случае пространственной задачи (рис. 2) направляющие косинусы вектора a = {ax ; ay ; az} можно найти воспользовавшись следующей формулой
| cos α = | ax | ; | cos β = | ay | ; | cos γ = | az |
| |a| | |a| | |a| |
Свойство:
cos2 α + cos2 β + cos2 γ = 1
 |
| рис. 2 |
Примеры задач с направляющими косинусами вектора
Примеры плоских задач с направляющими косинусами вектора
Пример 1. Найти направляющие косинусы вектора a = {3; 4}.
|a| = √32 + 42 = √9 + 16 = √25 = 5.
Найдем направляющие косинусы вектора a:
Решение:
Найдем модуль вектора a:|a| = √32 + 42 = √9 + 16 = √25 = 5.
Найдем направляющие косинусы вектора a:
| cos α = | ax | = | 3 | = 0.6 |
| |a| | 5 |
| cos β = | ay | = | 4 | = 0.8 |
| |a| | 5 |
Ответ: направляющие косинусы вектора cos α = 0.6, cos β = 0.8.
Пример 2. Найти значение векора a если его длина равна 26, а направляющие косинусы cos α = 5/13, cos β = -12/13.
5 13
ay = |a| · cos β = 26 · (-12 13
Решение:
ax = |a| · cos α = 26 ·ay = |a| · cos β = 26 · (-
Ответ: a = {10; -24}.
Примеры пространственных задач с направляющими косинусами вектора
Пример 3. Найти направляющие косинусы вектора a = {2; 4; 4}.
|a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Найдем направляющие косинусы вектора a:
Ответ: направляющие косинусы вектора cos α =1 3 2 3 2 3
Решение:
Найдем модуль вектора a:|a| = √22 + 42 + 42 = √4 + 16 + 16 = √36 = 6.
Найдем направляющие косинусы вектора a:
| cos α = | ax | = | 2 | = | 1 |
| |a| | 6 | 3 |
| cos β = | ay | = | 4 | = | 2 |
| |a| | 6 | 3 |
| cos γ = | az | = | 4 | = | 2 |
| |a| | 6 | 3 |
Ответ: направляющие косинусы вектора cos α =
Вектора
Вектор: определение и основные понятия
Определение координат вектора заданного координатами его начальной и конечной точки
Модуль вектора. Длина вектора
Направляющие косинусы вектора
Равенство векторов
Ортогональность векторов
Коллинеарность векторов
Компланарность векторов
Угол между векторами
Проекция вектора
Сложение и вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Линейно зависимые и линейно независимые вектора
Разложение вектора по базису
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
