Векторное произведение векторов.
Навигация по странице:
Определение. Векторным произведением вектора a на вектор b называется вектор c, длина которого численно равна площади параллелограмма построенного на векторах a и b, перпендикулярный к плоскости этих векторов и направленный так, чтоб наименьшее вращение от a к b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора c (рис. 1).
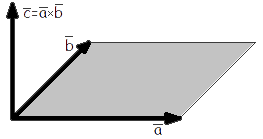 |
| рис. 1 |
Формулы вычисления векторного произведения векторов
Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат - это вектор, значение которого можно вычислить, используя следующие формулы:
a × b =
i j k ax ay az bx by bz
a × b = {aybz - azby; azbx - axbz; axby - aybx}
Свойства векторного произведения векторов
- Геометрический смысл векторного произведения.Модуль векторного произведения двух векторов a и b равен площади параллелограмма построенного на этих векторах:Sпарал = [a × b]
- Геометрический смысл векторного произведения.Площадь треугольника построенного на векторах a и b равна половине модуля векторного произведения этих векторов:
SΔ = 1 |a × b| 2 - Векторное произведения двух не нулевых векторов a и b равно нулю тогда и только тогда, когда вектора коллинеарны.
- Вектор c, равный векторному произведению не нулевых векторов a и b, перпендикулярен этим векторам.
- a × b = -b × a
- (k a) × b = a × (k b) = k (a × b)
- (a + b) × c = a × c + b × c
Примеры задач на вычисления векторного произведения векторов
Пример 1. Найти векторное произведение векторов a = {1; 2; 3} и b = {2; 1; -2}.
= i(2 · (-2) - 3 · 1) - j(1 · (-2) - 2 · 3) + k(1 · 1 - 2 · 2) =
= i(-4 - 3) - j(-2 - 6) + k(1 - 4) = -7i + 8j - 3k = {-7; 8; -3}
Решение:
| a × b = | i | j | k | = |
| 1 | 2 | 3 | ||
| 2 | 1 | -2 |
= i(2 · (-2) - 3 · 1) - j(1 · (-2) - 2 · 3) + k(1 · 1 - 2 · 2) =
= i(-4 - 3) - j(-2 - 6) + k(1 - 4) = -7i + 8j - 3k = {-7; 8; -3}
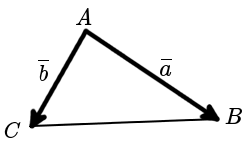
Решение: Найдем векторное произведение этих векторов:
| a × b = | i | j | k | = |
| -1 | 2 | -2 | ||
| 2 | 1 | -1 |
= i(2 · (-1) - (-2) · 1) - j((-1) · (-1) - (-2) · 2) + k((-1) · 1 - 2 · 2) =
= i(-2 + 2) - j(1 + 4) + k(-1 - 4) = -5j - 5k = {0; -5; -5}
Из свойств векторного произведения:
SΔ =Ответ: SΔ = 2.5√2.
Вектора
Вектор: определение и основные понятия
Определение координат вектора заданного координатами его начальной и конечной точки
Модуль вектора. Длина вектора
Направляющие косинусы вектора
Равенство векторов
Ортогональность векторов
Коллинеарность векторов
Компланарность векторов
Угол между векторами
Проекция вектора
Сложение и вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Линейно зависимые и линейно независимые вектора
Разложение вектора по базису
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
