Ортогональность векторов. Перпендикулярность векторов.
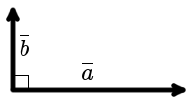 |
| рис. 1 |
Примеры задач на ортогональность векторов
Примеры плоских задач на ортогональность векторов
Так в случае плоской задачи для векторов a = {ax; ay} и b = {bx; by}, условие ортогональности запишется следующим образом:
Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) = 2 - 2 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 3 · 7 + (-1) · 5 = 21 - 5 = 16Ответ: так как скалярное произведение не равно нулю, то вектора a и b не ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 = 2n + 42n + 4 = 0
2n = -4
n = -2
Ответ: вектора a и b будут ортогональны при n = -2.
Примеры пространственных задач на ортогональность векторов
Так в случае пространственной задачи для векторов a = {ax; ay; az} и b = {bx; by; bz}, условие ортогональности запишется следующим образом:
Решение:
Найдем скалярное произведение этих векторов:
a · b = 1 · 2 + 2 · (-1) + 0 · 10 = 2 - 2 + 0 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · 3 + 3 · 1 + 1 · (-9) = 6 + 3 -9 = 0Ответ: так как скалярное произведение равно нулю, то вектора a и b ортогональны.
Решение:
Найдем скалярное произведение этих векторов:
a · b = 2 · n + 4 · 1 + 1 · (-8)= 2n + 4 - 8 = 2n - 42n - 4 = 0
2n = 4
n = 2
Ответ: вектора a и b будут ортогональны при n = 2.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
