Вектор: определение и основные понятия
Навигация по странице:
Определение вектора
Определение. Вектор - это направленный отрезок, то есть отрезок, имеющий длину и определенное направление. Графически вектора изображаются в виде направленных отрезков прямой определенной длины. (рис.1)
 |
| рис. 1 |
Обозначение вектора
Вектор началом которого есть точка А, а концом - точка В, обозначается AB (рис.1). Также вектора обозначают одной маленькой буквой, например a.
Длина вектора
Определение. Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора или модулем вектора AB.
Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|.
Нулевой вектор
Определение. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают.
Нулевой вектор обычно обозначается как 0.
Длина нулевого вектора равна нулю.
Коллинеарные вектора
Определение. Вектора, параллельные одной прямой или лежащие на одной прямой называют коллинеарными векторами (рис. 2).
 |
| рис. 2 |
Сонаправленные вектора
Определение. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b (рис. 3).
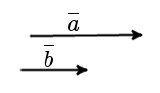 |
| рис. 3 |
Противоположно направленные вектора
Определение. Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b (рис. 4).
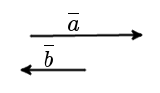 |
| рис. 4 |
Компланарные вектора
Определение. Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами. (рис. 5).
 |
| рис. 5 |
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные.
Равные вектора
Определение. Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны (рис. 6).
 |
| рис. 6 |
То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины:
a = b, если a↑↑b и |a| = |b|.
Единичный вектор
Определение. Единичным вектором или ортом - называется вектор, длина которого равна единице.
Вектора
Вектор: определение и основные понятия
Определение координат вектора заданного координатами его начальной и конечной точки
Модуль вектора. Длина вектора
Направляющие косинусы вектора
Равенство векторов
Ортогональность векторов
Коллинеарность векторов
Компланарность векторов
Угол между векторами
Проекция вектора
Сложение и вычитание векторов
Умножение вектора на число
Скалярное произведение векторов
Векторное произведение векторов
Смешанное произведение векторов
Линейно зависимые и линейно независимые вектора
Разложение вектора по базису
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
