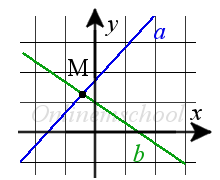
Пересечение прямых. Точка пересечения двух прямых

Методы решения. Существует два метода решения плоских задач на определение координат точки пересечения прямых:

• графический
• аналитический

Графический метод решения. Используя уравнения, начертить графики прямых и с помощью линейки найти координаты точки пересечения.

Аналитический метод решения. Необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны между собой)

Пример 1. Найти точку пересечения прямых y = 2x - 1 и y = -3x + 1.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2x - 1 y = -3x + 1

Вычтем из первого уравнения второе

y - y = 2x - 1 - (-3x + 1) y = -3x + 1     =>     0 = 5x - 2 y = -3x + 1

Из первого уравнения найдем значение x

5x = 2 y = -3x + 1     =>     x = 25 = 0.4 y = -3x + 1

Подставим значение x во второе уравнение и найдем значение y

x = 0.4 y = -3·(0.4) + 1 = -1.2 + 1 = -0.2

Ответ. Точка пересечения двух прямых имеет координаты (0.4, -0.2)

Пример 2. Найти точку пересечения прямых y = 2x - 1 и x = 2t + 1y = t.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

y = 2x - 1 x = 2t + 1 y = t

В первое уравнение подставим значения x и y из второго и третьего уравнений.

t = 2·(2t + 1) - 1 x = 2t + 1 y = t     =>     t = 4t + 1 x = 2t + 1 y = t     =>    

-3t = 1 x = 2t + 1 y = t     =>     t = -13 x = 2t + 1 y = t

Подставим значение t во второе и третье уравнение

t = -13 x = 2·(-13) + 1 = -23 + 1 = 13 y = -13

Ответ. Точка пересечения двух прямых имеет координаты (13, -13)

Пример 3 Найти точку пересечения прямых 2x + 3y = 0 и x - 23 = y4.

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

2x + 3y = 0 x - 23 = y4

Из второго уравнения выразим y через x

2x + 3y = 0 y = 4·x - 23

Подставим y в первое уравнение

2x + 3·4·x - 23 = 0 y = 4·x - 23     =>     2x + 4·(x - 2) = 0 y = 4·x - 23     =>    

2x + 4x - 8 = 0 y = 4·x - 23     =>     6x = 8 y = 4·x - 23     =>    

x = 86 = 43 y = 4·x - 23     =>     x = 86 = 43 y = 4·4/3 - 23 = 4·-2/3 3 = -89

Ответ. Точка пересечения двух прямых имеет координаты (43, -89)

Пример 4. Найти точку пересечения прямых y = 2x - 1 и y = 2x + 1.

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k₁ = k₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

y = 2x - 1 y = 2x + 1

Вычтем из первого уравнения второе

y - y = 2x - 1 - (2x + 1) y = -3x + 1     =>     0 = -2 y = -3x + 1

В первом уравнении получили противоречие (0 ≠ -2), значит система не имеет решений - отсутствуют точки пересечения прямых (прямые параллельны).

Ответ. Прямые не пересекаются (прямые параллельны).

Пример 5. Проверить является ли точка N(1, 1) точкой пересечения прямых y = x и y = 3x - 2.

Решение: Подставим координаты точки N в уравнения прямых.

1 = 1

1 = 3·1 - 2 = 1

Ответ. Так как оба уравнения превратились в тождества, то точка N - точка пересечения этих прямых.

Метод решения. Для определение координат точки пересечения прямых в пространстве, необходимо объединить уравнения прямых в систему, решение которой, позволит определить точные координаты точки пересечения прямых.

Если система уравнений:

• имеет единственное решение, то прямые пересекаются;
• имеет бесконечное множество решений, то прямые совпадают;
• не имеет решений, то прямые не пересекаются (прямые параллельны или скрещиваются между собой)

Пример 6. Найти точку пересечения прямых x - 1 = y - 1 = z - 1 и x - 3-2 = 2 - y = z.

Решение: Составим систему уравнений

x - 1 = a y - 1 = a z - 1 = a x - 3-2 = b 2 - y = b z = b   =>   x = a + 1 y = a + 1 z = a + 1 x - 3-2 = b 2 - y = b z = b   =>  

Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = a + 1 y = a + 1 z = a + 1 a + 1 - 3-2 = b 2 - (a + 1) = b a + 1 = b   =>   x = a + 1 y = a + 1 z = a + 1 a - 2-2 = b 1 - a = b a + 1 = b

К шестому уравнению добавим пятое уравнение

x = a + 1 y = a + 1 z = a + 1 a - 2-2 = b 1 - a = b a + 1 + (1 - a) = b + b   =>   x = a + 1 y = a + 1 z = a + 1 a - 2-2 = b 1 - a = b b = 1

Подставим значение b в четвертое и пятое уравнения

x = a + 1 y = a + 1 z = a + 1 a - 2-2 = 1 1 - a = 1 b = 1   =>   x = a + 1 y = a + 1 z = a + 1 a - 2 = -2 a = 0 b = 1   =>  

x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1   =>   x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Замечание. Если уравнения прямых заданы параметрически, и в обоих уравнениях параметр задан одной и той же буквой, то при составлении системы в одном из уравнений необходимо заменить букву отвечающую за параметр.

Пример 7. Найти точку пересечения прямых x = 2t - 3 y = t z = -t + 2 и x = t + 1 y = 3t - 2 z = 3 .

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

x = 2t - 3 y = t z = -t + 2 x = a + 1 y = 3a - 2 z = 3

Подставим значения x, y, z из 1, 2, 3 уравнений в 4, 5, 6 уравнения

x = 2t - 3 y = t z = -t + 2 2t - 3 = a + 1 t = 3a - 2 -t + 2 = 3   =>   x = 2t - 3 y = t z = -t + 2 2t = a + 4 t = 3a - 2 t = -1   =>  

Подставим значение t из шестого уравнения в остальные уравнения

x = 2·(-1) - 3 y = (-1) z = -(-1) + 2 2·(-1) = a + 4 -1 = 3a - 2 t = -1   =>   x = -5 y = -1 z = 3 a = -6 a = 13 t = -1

Ответ. Так как -6 ≠ 13, то прямые не пересекаются.