Угол между плоскостями.
Навигация по странице:
Определение.
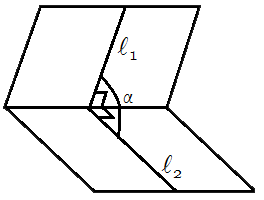
Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.Определение.
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
| cos α = | |A1·A2 + B1·B2 + C1·C2| |
| √A12 + B12 + C12√A22 + B22 + C22 |
Примеры задач на вычисление угла между плоскостями
Пример 1.
Найти угол между плоскостями 2x + 4y - 4z - 6 = 0 и 4x + 3y + 9 = 0.
Решение. Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:
cos α =Ответ: косинус угла между плоскостями равен cos α =
Аналитическая геометрия: Вступление и оглавлениеРасстояние между двумя точкамиСередина отрезка. Координаты середины отрезкаУравнение прямойТочка пересечения прямыхУгол между прямымиУравнение плоскостиРасстояние от точки до плоскостиРасстояние между плоскостямиРасстояние от точки до прямой на плоскостиРасстояние от точки до прямой в пространствеУгол между плоскостямиУгол между прямой и плоскостью
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
|
0
|
||||
