Расстояние между двумя точками
Навигация по странице:
Определение. Расстояние между двумя точками — это длина отрезка, что соединяет эти точки.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления расстояния между двумя точками A(xa, ya) и B(xb, yb) на плоскости:
AB = √(xb - xa)2 + (yb - ya)2 - Формула вычисления расстояния между двумя точками A(xa, ya, za) и B(xb, yb, zb) в пространстве:
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2
Вывод формулы для вычисления расстояния между двумя точками на плоскости
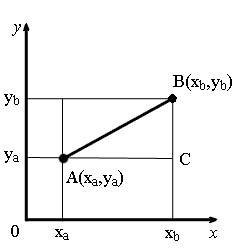
Из точек A и B опустим перпендикуляры на оси координат.
Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:
AC = xb - xa;
BC = yb - ya.
Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:
AB = √AC2 + BC2.
Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.
Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.
Примеры задач на вычисление расстояния между двумя точками
Примеры вычисления расстояния между двумя точками на плоскости
Пример 1.
Найти расстояние между точками A(-1, 3) и B(6,2).
Решение.
AB = √(xb - xa)2 + (yb - ya)2 = √(6 - (-1))2 + (2 - 3)2 = √72 + 12 = √50 = 5√2
Ответ: AB = 5√2.
Пример 2.
Найти расстояние между точками A(0, 1) и B(2,-2).
Решение.
AB = √(xb - xa)2 + (yb - ya)2 = √(2 - 0)2 + (-2 - 1)2 = √22 + (-3)2 = √13
Ответ: AB = √13.
Примеры вычисления расстояния между двумя точками в пространстве
Пример 3.
Найти расстояние между точками A(-1, 3, 3) и B(6, 2, -2).
Решение.
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2 =
= √(6 - (-1))2 + (2 - 3)2 + (-2 - 3)2 = √72 + 12 + 52 = √75 = 5√3
= √(6 - (-1))2 + (2 - 3)2 + (-2 - 3)2 = √72 + 12 + 52 = √75 = 5√3
Ответ: AB = 5√3.
Пример 4.
Найти расстояние между точками A(0, -3, 3) и B(3, 1, 3).
Решение.
AB = √(xb - xa)2 + (yb - ya)2 + (zb - za)2 =
= √(3 - 0)2 + (1 - (-3))2 + (3 - 3)2 = √32 + 42 + 02 = √25 = 5
= √(3 - 0)2 + (1 - (-3))2 + (3 - 3)2 = √32 + 42 + 02 = √25 = 5
Ответ: AB = 5.
Аналитическая геометрия: Вступление и оглавлениеРасстояние между двумя точкамиСередина отрезка. Координаты середины отрезкаУравнение прямойТочка пересечения прямыхУгол между прямымиУравнение плоскостиРасстояние от точки до плоскостиРасстояние между плоскостямиРасстояние от точки до прямой на плоскостиРасстояние от точки до прямой в пространствеУгол между плоскостямиУгол между прямой и плоскостью
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
