Определитель матрицы.

Навигация по странице:

Определение определителя матрицы
Свойства определителя матрицы
Методы вычисления определителя матрицы

Онлайн калькулятор. Определитель матрицы.

Определитель матрицы или детерминант матрицы - это одна из основных численных характеристик квадратной матрицы, применяемая при решении многих задач.

Определение.

Определителем матрицы n×n будет число:

det(A) =	Σ	(-1)^{N(α₁,α₂,...,α_n)}·a_α₁1·a_α₂2·...·a_{α_nn}
	(α₁,α₂,...,α_n)

где (α₁,α₂,...,α_n) - перестановка чисел от 1 до n, N(α₁,α₂,...,α_n) - число инверсий в перестановке, суммирование идёт по всем возможным перестановкам порядка n.

Обозначение

Определитель матрици A обычно обозначается det(A), |A|, или ∆(A).

Свойства определителя матрицы

Определитель единичной матрицы равен единице:
det(E) = 1
Определитель матрицы с двумя равными строками (столбцами) равен нулю.
Определитель матрицы с двумя пропорциональными строками (столбцами) равен нулю.
Определитель матрицы, содержащий нулевую строку (столбец), равен нулю.
Определитель матрицы равен нулю если две (или несколько) строк (столбцев) матрицы линейно зависимы.
При транспонировании значение определителя матрицы не меняется:
det(A) = det(A^T)
Определитель обратной матрицы:
det(A^-1) = det(A)^-1
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить другую строку (столбец), умноженную на некоторое число.
Определитель матрицы не изменится, если к какой-то его строке (столбцу) прибавить линейную комбинации других строк (столбцов).
Если поменять местами две строки (столбца) матрицы, то определитель матрицы поменяет знак.
Общий множитель в строке (столбце) можно выносить за знак определителя:
a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... k·a_i1k·a_i2...k·a_in .... a_n1a_n2...a_nn = k· a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... a_i1a_i2...a_in .... a_n1a_n2...a_nn
Если квадратная матрица n-того порядка умножается на некоторое ненулевое число, то определитель полученной матрицы равен произведению определителя исходной матрицы на это число в n-той степени:
B = k·A => det(B) = kⁿ·det(A)
где A матрица n×n, k - число.
Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем:

a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... b_i1 + c_i1b_i2 + c_i2...b_in + c_in .... a_n1a_n2...a_nn = a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... b_i1b_i2...b_in .... a_n1a_n2...a_nn + a₁₁a₁₂...a_1n a₂₁a₂₂...a_2n .... c_i1c_i2...c_in .... a_n1a_n2...a_nn
Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.
Определитель произведения матриц равен произведению определителей этих матриц:
det(A·B) = det(A)·det(B)

Методы вычисления определителя матрицы

Вычисление определителя матрицы 1×1

Правило:

Для матрицы первого порядка значение определителя равно значению элемента этой матрицы:

∆ = |a₁₁| = a₁₁

Вычисление определителя матрицы 2×2

Правило:

Для матрицы 2×2 значение определителя равно разности произведений элементов главной и побочной диагоналей:

∆ =

a₁₁	a₁₂
a₂₁	a₂₂

= a₁₁·a₂₂ - a₁₂·a₂₁

Пример 1.

Найти определитель матрицы A

A =

	5	7
	-4	1

Решение:

det(A) =

5	7
-4	1

= 5·1 - 7·(-4) = 5 + 28 = 33

Вычисление определителя матрицы 3×3

Правило треугольника для вычисления определителя матрицы 3-тего порядка

Правило:

Для матрицы 3×3 значение определителя равно сумме произведений элементов главной диагонали и произведений элементов лежащих на треугольниках с гранью параллельной главной диагонали, от которой вычитается произведение элементов побочной диагонали и произведение элементов лежащих на треугольниках с гранью параллельной побочной диагонали.


+		–

∆ =

a₁₁	a₁₂	a₁₃
a₂₁	a₂₂	a₂₃
a₃₁	a₃₂	a₃₃

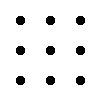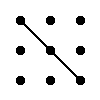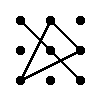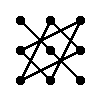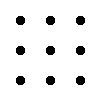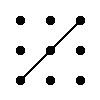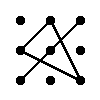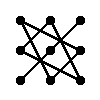= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Правило Саррюса для вычисления определителя матрицы 3-тего порядка

Правило:

Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком "плюс"; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком "минус":

∆ =

a₁₁	a₁₂	a₁₃	a₁₁	a₁₂
a₂₁	a₂₂	a₂₃	a₂₁	a₂₂
a₃₁	a₃₂	a₃₃	a₃₁	a₃₂

= a₁₁·a₂₂·a₃₃ + a₁₂·a₂₃·a₃₁ + a₁₃·a₂₁·a₃₂ - a₁₃·a₂₂·a₃₁ - a₁₁·a₂₃·a₃₂ - a₁₂·a₂₁·a₃₃

Пример 2.

Найти определитель матрицы A = 571 -410 203

Решение:

det(A) = 571 -410 203 = 5·1·3 + 7·0·2 + 1·(-4)·0 - 1·1·2 - 5·0·0 - 7·(-4)·3 = 15 + 0 + 0 - 2 - 0 + 84 = 97

Вычисление определителя матрицы произвольного размера

Разложение определителя по строке или столбцу

Правило:

Определитель матрицы равен сумме произведений элементов строки определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	- разложение по i-той строке
	j = 1

Правило:

Определитель матрицы равен сумме произведений элементов столбца определителя на их алгебраические дополнения:

	n
det(A) =	Σ	a_ij·A_ij	- разложение по j-тому столбцу
	i = 1

При разложение определителя матрицы обычно выбирают ту строку/столбец, в которой/ом максимальное количество нулевых элементов.

Пример 3.

Найти определитель матрицы A

A =

2	4	1
0	2	1
2	1	1

Решение: Вычислим определитель матрицы разложив его по первому столбцу:

det(A) =

2	4	1
0	2	1
2	1	1

= 2·(-1)¹⁺¹· 21 11 + 0·(-1)²⁺¹· 41 11 + 2·(-1)³⁺¹· 41 21 =

= 2·(2·1 - 1·1) + 2·(4·1 - 2·1) = 2·(2 - 1) + 2·(4 - 2) = 2·1 + 2·2 = 2 + 4 = 6

Пример 4.

Найти определитель матрицы A

A = 2411 0200 2113 4023

Решение: Вычислим определитель матрицы, разложив его по второй строке (в ней больше всего нулей):

det(A) = 2411 0200 2113 4023 = - 0· 411 113 023 + 2· 211 213 423 - 0· 241 213 403 + 0· 241 211 402 =

= 2·(2·1·3 + 1·3·4 + 1·2·2 - 1·1·4 - 2·3·2 - 1·2·3) = 2·(6 +12 + 4 - 4 - 12 - 6) = 2·0 = 0

Приведение определителя к треугольному виду

Правило:

Используя свойства определителя для элементарных преобразований над строками и столбцами 8 - 11, определитель приводится к треугольному виду, и тогда его значение будет равно произведению элементов стоящих на главной диагонали.

Пример 5.

Найти определитель матрицы A приведением его к треугольному виду

A = 2411 0210 2113 4023

Решение:

det(A) = 2411 0210 2113 4023

Сначала получим нули в первом столбце под главной диагональю. Для этого отнимем от 3-тей строки 1-ую строку, а от 4-той строки 1-ую строку, умноженную на 2:

det(A) = 2411 0210 2 - 21 - 41 - 13 - 1 4 - 2·20 - 4·22 - 1·23 - 1·2 = 2411 0210 0-302 0-801

Получим нули во втором столбце под главной диагональю. Для этого поменяем местами 2-ой и 3-тий столбцы (при этом детерминант сменит знак на противоположный):

det(A) = - 2141 0120 00-32 00-81

Получим нули в третьем столбце под главной диагональю. Для этого к 3-ему столбцу добавим 4-тий столбец, умноженный на 8:

det(A) = - 214 + 1·81 012 + 0·80 00-3 + 2·82 00-8 + 1·81 = - 21121 0120 00132 0001 = -2·1·13·1 = -26

Теорема Лапласа

Теорема:

Пусть ∆ - определитель n-ого порядка. Выберем в нем произвольные k строк (столбцов), причем k < n. Тогда сумма произведений всех миноров k-ого порядка, которые содержатся в выбранных строках (столбцах), на их алгебраические дополнения равна определителю.

Онлайн калькуляторы с матрицами.

Упражнения с матрицами.

Матрицы. вступление и оглавление Матрицы: определение и основные понятия.Сведение системы линейных уравнений к матрице.Виды матриц Умножение матрицы на число.Сложение и вычитание матриц.Умножение матриц.Транспонирование матрицы.Элементарные преобразования матрицы.Определитель матрицы.Минор и алгебраическое дополнение матрицы.Обратная матрица.Линейно зависимые и независимые строки.Ранг матрицы.

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!