OnlineMSchool
Изучение математики онлайн.
Изучайте математику с нами и убедитесь: "Математика - это просто!"
Регистрация Войти Выйти

Квадрат. Формулы и свойства квадрата

Навигация по странице: Определение квадрата Основные свойства квадрата Диагональ квадрата Периметр квадрата Площадь квадрата Окружность описанная вокруг квадрата Окружность вписанная в квадрат
Определение.
Квадрат - это четырехугольник у которого все четыре стороны и углы одинаковы. Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.
Изображение квадрата с обозначениями Изображение квадрата с обозначениями
Рис.1 Рис.2

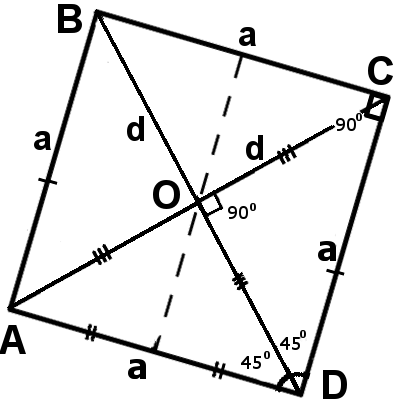
Основные свойства квадрата

Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.
1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:

AB = BC = CD = AD

2. Противоположные стороны квадрата параллельны:

AB||CD,   BC||AD

3. Все четыре угла квадрата прямые:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Сумма углов квадрата равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

5. Диагонали квадрата имеют одинаковой длины:

AC = BD

6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры
7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:

AC┴BD        AO = BO = CO = DO =  d
2
8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности
9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:

ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°

10. Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:

ΔAOB = ΔBOC = ΔCOD = ΔDOA


Диагональ квадрата

Определение.
Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата.
Диагональ любого квадрата всегда больше его стороны в√2 раз.

Формулы определения длины диагонали квадрата

1. Формула диагонали квадрата через сторону квадрата:

d = a·√2

2. Формула диагонали квадрата через площадь квадрата:

d = √2S

3. Формула диагонали квадрата через периметр квадрата:
d = P
2√2
4. Формула диагонали квадрата через радиус описанной окружности:

d = 2R

5. Формула диагонали квадрата через диаметр описанной окружности:

d = Dо

6. Формула диагонали квадрата через радиус вписанной окружности:

d = 2r√2

7. Формула диагонали квадрата через диаметр вписанной окружности:

d = Dв√2

8. Формула диагонали квадрата через длину отрезка l:
d = l 2√10
5

Периметр квадрата

Определение.
Периметром квадрата называется сумма длин всех сторон квадрата.

Формулы определения длины периметра квадрата

1. Формула периметра квадрата через сторону квадрата:

P = 4a

2. Формула периметра квадрата через площадь квадрата:

P = 4√S

3. Формула периметра квадрата через диагональ квадрата:

P = 2d√2

4. Формула периметра квадрата через радиус описанной окружности:

P = 4R√2

5. Формула периметра квадрата через диаметр описанной окружности:

P = 2Dо√2

6. Формула периметра квадрата через радиус вписанной окружности:

P = 8r

7. Формула периметра квадрата через диаметр вписанной окружности:

P = 4Dв

8. Формула периметра квадрата через длину отрезка l:
P = l 8
√5

Площадь квадрата

Определение.
Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.
Площадь квадрата больше площади любого четырехугольника с таким же периметром.

Формулы определения площади квадрата

1. Формула площади квадрата через сторону квадрата:

S = a2

2. Формула площади квадрата через периметр квадрата:
S = P2
16
3. Формула площади квадрата через диагональ квадрата:
S = d2
2
4. Формула площади квадрата через радиус описанной окружности:

S = 2R2

5. Формула площади квадрата через диаметр описанной окружности:
S = Do2
2
6. Формула площади квадрата через радиус вписанной окружности:

S = 4r2

7. Формула площади квадрата через диаметр вписанной окружности:

S = Dв2

8. Формула площади квадрата через длину отрезка l:
S = l 2 16
√5

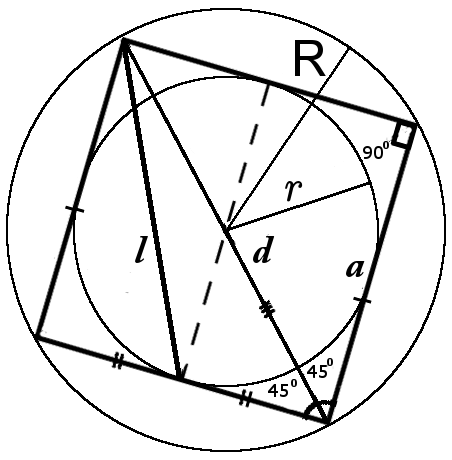
Окружность описанная вокруг квадрата

Определение.
Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.

Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз.

Радиус окружности описанной вокруг квадрата равен половине диагонали.

Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.

Формулы определения радиуса окружности описанной вокруг квадрата

1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:
R = a √2
2
2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:
R = P
4√2
3. Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:
R = √2S
2
4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:
R = d
2
5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:
R = Dо
2
6. Формула радиуса круга описанного вокруг квадрата через радиус вписанной окружности:

R = r √2

7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:
R = Dв √2
2
8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:
R = l √10
5

Окружность вписанная в квадрата

Определение.
Кругом вписанным в квадрат называется круг, который примыкает к серединам сторон квадрата и имеет центр на пересечении диагоналей квадрата.

Радиус вписанной окружности равен половине стороны квадрата.

Площадь круга вписанного в квадрат меньше площади квадрата в 4/π раза.

Формулы определения радиуса круга вписанного в квадрат

1. Формула радиуса круга вписанного в квадрат через сторону квадрата:
r = a
2
2. Формула радиуса круга вписанного в квадрат через диагональ квадрата:
r = d
2√2
3. Формула радиуса круга вписанного в квадрат через периметр квадрата:
r = P
8
4. Формула радиуса круга вписанного в квадрат через площадь квадрата:
r = √S
2
5. Формула радиуса круга вписанного в квадрат через радиус описанной окружности:
r = R
√2
6. Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности:
r = Dо
2√2
7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности:
r = Dв
2
8. Формула радиуса круга вписанного в квадрат через длину отрезка l:
r = l
√5
Формулы по геометрии Треугольник. Формулы и свойства треугольника Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Правильный многоугольник. Формулы и свойства правильного многоугольника Окружность, круг, сегмент, сектор. Формулы и свойства Эллипс. Формулы и свойства эллипса Куб. Формулы и свойства куба Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда Призма. Формулы и свойства призмы Пирамида. Формулы и свойства пирамиды Сфера, шар, сегмент и сектор. Формулы и свойства Цилиндр. Формулы и свойства Конус. Формулы и свойства Формулы площади геометрических фигур S Формулы периметра геометрических фигур P Формулы объема геометрических фигур V Формулы площади поверхности геометрических фигур S
Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0
Присоединяйтесь