Равнобедренная трапеция. Формулы, признаки и свойства равнобедренной трапеции

Формулы и свойства трапеции

Определение.

Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.

На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.

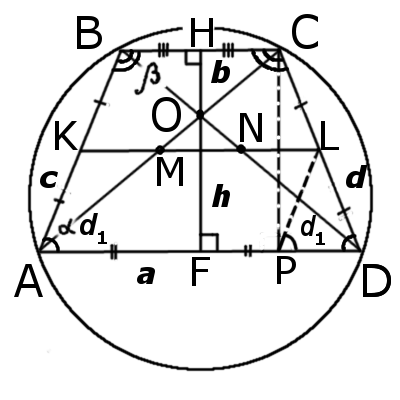Изображение равнобедренной трапеции с обозначениями

Рис.1

Признаки равнобедренной трапеции

Трапеция будет равнобедренной если выполняется одно из этих условий:

1. Углы при основе равны:

∠ABC = ∠BCD и ∠BAD = ∠ADC

2. Диагонали равны:

AC = BD

3. Одинаковые углы между диагоналями и основаниями:

∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC

4. Сумма противоположных углов равна 180°:

∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°

5. Вокруг трапеции можно описати окружность

Основные свойства равнобедренной трапеции

1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:

∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°

2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:

AB = CD = m

3. Вокруг равнобедренной трапеции можно описать окружность

4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):

h = m

5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:

S_ABCD = h²

6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:

h² = BC · AD

7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:

AC² + BD² = AB² + CD² + 2BC · AD

8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:

HF ┴ BC, HF ┴ AD

9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) - равен полуразности оснований:

AP =	BC + AD
	2

PD =	AD - BC
	2

10. Также смотрите свойства трапеции

Стороны равнобедренной трапеции

Формулы длин сторон равнобедренной трапеции:

1. Формулы длины сторон через другие стороны, высоту и угол:

a = b + 2h ctg α = b + 2c cos α

b = a - 2h ctg α = a - 2c cos α

c =	h	=	a - b
	sin α		2 cos α

2. Формула длины сторон трапеции через диагонали и другие стороны:

a =	d₁² - c²	b =	d₁² - c²	c = √d₁² - ab
	b		a

3. Формулы длины основ через площадь, высоту и другую основу:

a =	2S	- b b =	2S	- a
	h		h

4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:

с =	S
	m sin α

5. Формулы длины боковой стороны через площадь, основания и угол при основе:

с =	2S
	(a + b) sin α

Средняя линия равнобедренной трапеции

Формулы длины средней линии равнобедренной трапеции:

1. Формула определения длины средней линии через основания, высоту и угол при основании:

m = a - h ctg α = b + h ctg α = a - √c² - h² = b + √c² - h²

2. Формула средней линии трапеции через площадь и сторону:

m =	S
	c sin α

Высота равнобедренной трапеции

Формулы определения длины высоты равнобедренной трапеции:

1. Формула высоты через стороны:

h =	1	√4c² - (a - b)²
	2

2. Формула высоты через стороны и угол прилегающий к основе:

h =	a - b	tg β	= c sin β
	2

Диагонали равнобедренной трапеции

Диагонали равнобедренной трапеции равны:

d₁ = d₂

Формулы длины диагоналей равнобедренной трапеции:

1. Формула длины диагонали через стороны:

d₁ = √с² + ab

2. Формулы длины диагонали по теореме косинусов:

d₁ = √a² + c² - 2ac cos α

d₁ = √b² + c² - 2bc cos β

3. Формула длины диагонали через высоту и среднюю линию:

d₁ = √h² + m²

4. Формула длины диагонали через высоту и основания:

d₁ =	1	√4h² + (a + b)²
	2

Площадь равнобедренной трапеции

Формулы площади равнобедренной трапеции:

1. Формула площади через стороны:

S =	a + b	√4c² - (a - b)²
	4

2. Формула площади через стороны и угол:

S = (b + c cos α) c sin α = (a - c cos α) c sin α

3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:

S =	4 r ²	=	4 r ²
	sin α		sin β

4. Формула площади через основания и угол между основой и боковой стороной:

S =	ab	=	ab
	sin α		sin β

5. Формула площади ранобедренной трапеции в которую можно вписать окружность:

S = (a + b) · r = √ab·c = √ab·m

6. Формула площади через диагонали и угол между ними:

S =	d₁²	· sin γ	=	d₁²	· sin δ
	2			2

7. Формула площади через среднюю линию, боковую сторону и угол при основании:

S = mc sin α = mc sin β

8. Формула площади через основания и высоту:

S =	a + b	· h
	2

Окружность описанная вокруг трапеции

Окружность можно описать только вокруг равнобедренной трапеции!!!

Формула определения радиуса описанной вокруг трапеции окружности:

1. Формула радиуса через стороны и диагональ:

R =	a·c·d₁
	4√p(p - a)(p - c)(p - d₁)

где

p =	a + c + d₁
	2

a - большее основание

Формулы по геометрии Треугольник. Формулы и свойства треугольника

Квадрат. Формулы и свойства квадрата

Прямоугольник. Формулы и свойства прямоугольника

Параллелограмм. Формулы и свойства параллелограмма

Ромб. Формулы и свойства ромба

Трапеция. Формулы и свойства трапеции

- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции

- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции

Правильный многоугольник. Формулы и свойства правильного многоугольника

Окружность, круг, сегмент, сектор. Формулы и свойства

Эллипс. Формулы и свойства эллипса

Куб. Формулы и свойства куба

Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда Призма. Формулы и свойства призмы

Пирамида. Формулы и свойства пирамиды

Сфера, шар, сегмент и сектор. Формулы и свойства

Цилиндр. Формулы и свойства

Конус. Формулы и свойства

Формулы площади геометрических фигур S Формулы периметра геометрических фигур P Формулы объема геометрических фигур V Формулы площади поверхности геометрических фигур S

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!