Логарифмические неравенства

Определение. Логарифмические неравенства - это неравенства, содержащие переменную под знаком логарифма.

Например: log₃ (x² - 3 x + 3) > 1.

При решении логарифмических неравенств помним:

общие свойства неравенств;
свойства монотонности логарифмической функции;
область определения логарифмической функции.

Основные методы решения логарифмических неравенств

log_a f(x) > b a > 1 <=> f(x) > a^b
log_a f(x) > b 0 < a < 1 <=> 0 < f(x) < a^b
log_a f(x) < b a > 1 <=> 0 < f(x) < a^b
log_a f(x) < b 0 < a < 1 <=> f(x) > a^b
log_g(x) f(x) > b <=> f(x) > g(x)^b g(x) > 1 f(x) < g(x)^b 0 < g(x) < 1 f(x) > 0
log_g(x) f(x) < b <=> f(x) < g(x)^b g(x) > 1 f(x) > 0 f(x) > g(x)^b 0 < g(x) < 1
log_a f(x) > log_a h(x) a > 1 <=> f(x) > h(x) h(x) > 0
log_a f(x) > log_a h(x) 0 < a < 1 <=> f(x) < h(x) f(x) > 0
log_a f(x) < log_a h(x) a > 1 <=> f(x) < h(x) f(x) > 0
log_a f(x) < log_a h(x) 0 < a < 1 <=> f(x) > h(x) h(x) > 0
log_g(x) f(x) > log_g(x) h(x) <=> f(x) > h(x) g(x) > 1 h(x) > 0 f(x) < h(x) 0 < g(x) < 1 f(x) > 0
log_g(x) f(x) < log_g(x) h(x) <=> f(x) < h(x) g(x) > 1 f(x) > 0 f(x) > h(x) 0 < g(x) < 1 h(x) > 0

Примеры решения логарифмических неравенств

Пример 1.

Решить неравенство log₂ (x² + 3x) ≤ 2.

Так как основа логарифма 2 > 1, то используем третий метод для решения неравенства

log₂ (x² + 3x) ≤ 2 => 0 < x² + 3x ≤ 2² => x² + 3x ≤ 4 x² + 3x > 0 => x² + 3x -4 ≤ 0 x(x + 3) > 0 => (x + 4)(x -1) ≤ 0 x(x + 3) > 0

Найдем общее решение:

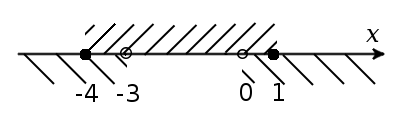
x ∈ [-4; -3) ∪ (0; 1]

Ответ: x ∈ [-4; -3) ∪ (0; 1].

Пример 2.

Решить неравенство log_{x - 3} (x - 1) < 2.

Используем вторую схему для решения неравенства

log_{x - 3} (x - 1) < 2 => x - 1 < (x - 3)² x - 3 > 1 x - 1 > 0 x - 1 > (x - 3)² 0 < x - 3 < 1 => x - 1 < x² - 6x + 9 x > 4 x > 1 x - 1 > x² - 6x + 9 3 < x < 4 => x² - 7x + 10 > 0 x > 4 x² - 7x + 10 < 0 3 < x < 4 => (x - 2)(x -5) > 0 x > 4 (x - 2)(x -5) < 0 3 < x < 4 => x ∈ (-∞; 2) ∪ (5; +∞) x > 4 x ∈ (2; 5) 3 < x < 4 => x ∈ (5; +∞) x ∈ (3; 4) => x ∈ (3; 4) ∪ (5; +∞)

Ответ: x ∈ (3; 4) ∪ (5; +∞).

Пример 3.

Решить неравенство log²_0.5 x + log_0.5 x - 2 ≤ 0.

ОДЗ x > 0.

Сделаем замену log_0.5 x = t

t² + t - 2 ≤ 0

(t + 2)(t - 1) ≤ 0

-2 ≤ t ≤ 1

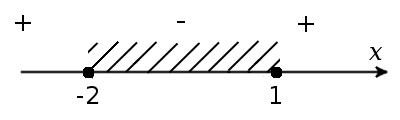
Вернемся обратно к переменной x и с учетом ОДЗ решим неравенство:

t ≥ -2 t ≤ 1 => log_0.5 x ≥ -2 log_0.5 x ≤ 1 =>

Так как основа логарифма 0.5 < 1

=> x ≤ 0.5^-2 x ≥ 0.5¹ => x ≤ 4 x ≥ 0.5

Ответ: x ∈ [0.5; 4].

Пример 4.

Решить неравенство: log_0.4 x + log_0.4 (x - 1) ≥ log_0.4 (x + 3).

ОДЗ: x > 0 x - 1 > 0 x + 3 > 0 => x > 0 x > 1 x > -3 => x > 1

Используя свойство, суммы логарифмов, перепишем неравенство:

log_0.4 x(x - 1) ≥ log_0.4 (x + 3)

Так как основа логарифма 0.4 < 1 используем 8 схему решения неравенств, с учетом ОДЗ:

x(x - 1) ≤ x + 3 x > 1 => x² - x ≤ x + 3 x > 1 => x² - 2x - 3 ≤ 0 x > 1 => (x + 1)(x - 3) ≤ 0 x > 1

Найдем общее решение:

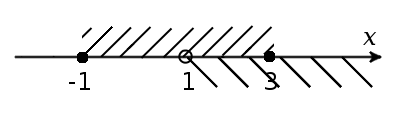
Ответ: x ∈ (1; 3].

Пример 5.

Решить неравенство: (3 - 2x) log_0.1 x < 0.

ОДЗ: x > 0

Найдем нули функции, стоящей в левой части неравенства:

(3 - 2x) log_0.1 x = 0 => 3 - 2x = 0 log_0.1 x = 0 => x = 1.5 x = 1

Используя метод интервалов найдем решение:

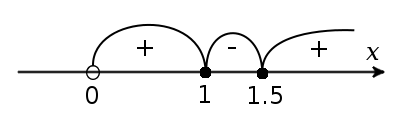
Ответ: x ∈ (1; 1.5).

Логарифмы Логарифм числа, основное логарифмическое тождество Формулы и свойства логарифмов Логарифм произведения. Сумма логарифмов Логарифм частного. Разность логарифмов Логарифм степени Логарифм корня Логарифмирование Потенцирование Десятичный логарифм Натуральный логарифм Число е Логарифмическая функция Логарифмические уравнения Логарифмические неравенства

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!