Конус. Формулы, признаки и свойства конуса

Навигация по странице: Определение конуса Элементы конуса Объём конуса Площадь поверхности конуса Уравнение конуса Основные свойства кругового конуса

Определение.

Конус — это геометрическое тело, которое образовано совокупностью всех лучей, исходящих из точки и пересекающих любую плоскую поверхность. В месте пересечения образуется основание конуса.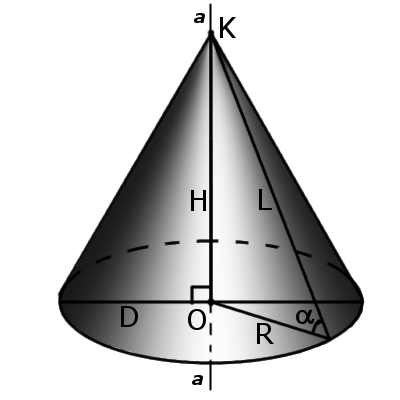


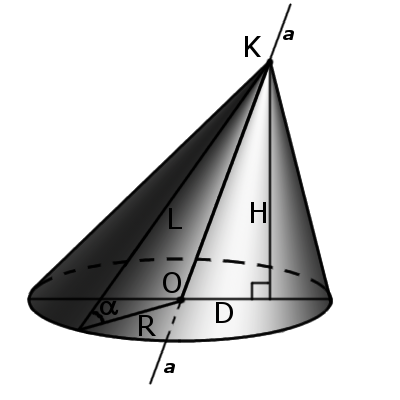
Рис.1		Рис.2



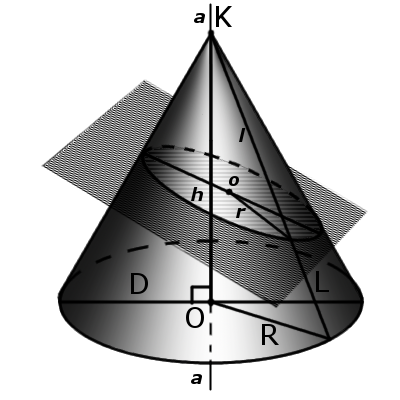
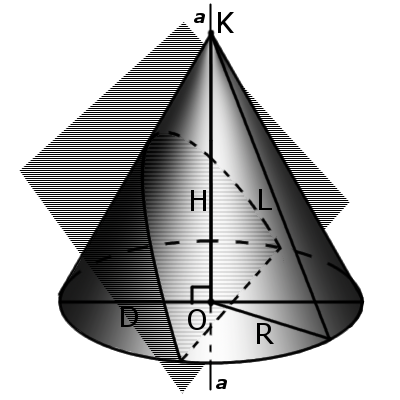
Рис.3		Рис.4

Элементы конуса

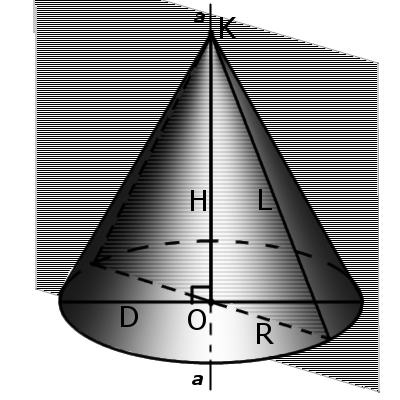
Определение. Вершина конуса - это точка (K), из которой исходят лучи.

Определение. Основание конуса - это плоскость, образованная в результате пересечения плоской поверхности и всех лучей, исходящих из вершины конуса. У конуса могут быть такие основы, как круг, эллипс, гипербола и парабола.

Определение. Образующей конуса (L) называется любой отрезок, который соединяет вершину конуса с границей основания конуса. Образующая есть отрезок луча, выходящего из вершины конуса.

Формула. Длина образующей (L) прямого кругового конуса через радиус R и высоту H (через теорему Пифагора):

L² = R² + H²

Определение. Направляющая конуса - это кривая, которая описывает контур основания конуса.

Определение. Боковая поверхность конуса - это совокупность всех образующих конуса. То есть, поверхность, которая образуется движением образующей по направляющей конуса.

Определение. Поверхность конуса состоит из боковой поверхности и основания конуса.

Определение. Высота конуса (H) - это отрезок, который выходит из вершины конуса и перпендикулярный к его основанию.

Определение. Ось конуса (a) - это прямая, проходящая через вершину конуса и центр основания конуса.

Определение. Конусность (С) конуса - это отношение диаметра основания конуса к его высоте. В случае усеченного конуса - это отношение разности диаметров поперечных сечений D и d усеченного конуса к расстоянию между ними:

C =	D	и C =	D - d
	H		h

где C - конусность, D - диаметр основания, d - диаметр меньшего основания и h - расстояние между основаниями.

Конусность характеризует остроту конуса, то есть, угол наклона образующей к основанию конуса. Чем больше конусность, тем острее угол наклона. угол конуса α будет:

α = 2arctg	R
	H

где R - радиус основы, а H - высота конуса.

Определение. Осевое сечение конуса - это сечение конуса плоскостью, проходящей через ось конуса. Такое сечение образует равнобедренный треугольник, у которого стороны образованы образующими, а основание треугольника - это диаметр основания конуса.

Определение. Касательная плоскость к конусу - это плоскость, проходящая через образующую конуса и перпендикулярна к осевому сечению конуса.

Определение. Конус, что опирается на круг, эллипс, гиперболу или параболу называется соответственно круговым, эллиптическим, гиперболическим или параболическим конусом (последние два имеют бесконечный объем).

Определение. Прямой конус - это конус у которого ось перпендикулярна основе. У такого конуса ось совпадает с высотой, а все образующие равны между собой.

Формула. Объём кругового конуса:

V =	1	πHR²
	3

где R - радиус основы, а H - высота конуса.

Формула. Площадь боковой поверхности (S_b) прямого конуса через радиус R и длину образующей L:

S_b = πRL

Формула. Общая площадь поверхности (S_p) прямого кругового конуса через радиус R и длину образующей L:

S_p = πRL + πR²

Определение. Косой (наклонный) конус - это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.

Формула. Объём любого конуса:

V =	1	SH
	3

где S - площадь основы, а H - высота конуса.

Определение. Усеченный конус - это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.

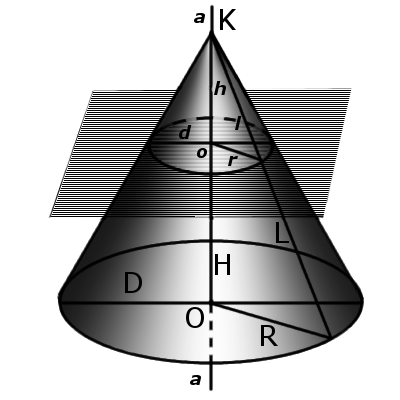
Формула. Объём усеченного конуса:

V =	1	(S₂H - S₁h)
	3

где S₁ и S₂ - площади меньшей и большей основы соответственно, а H и h - расстояние от вершины конуса до центра нижней и верхней основы соответственно.

Уравнение конуса

1. Уравнение прямого кругового конуса в декартовой системе координат с координатами (x, y, z):

x²	+	y²	-	z²	= 0
a²		a²		c²

2. Уравнение прямого эллиптического конуса в декартовой системе координат с координатами (x, y, z):

x²	+	y²	=	z²
a²	+	b²	=	c²

Основные свойства кругового конуса

1. Все образующие прямого кругового конуса равны между собой.

2. При вращении прямоугольного треугольника вокруг своего катета на 360 ° образуется прямой круговой конус.

3. При вращении равнобедренного треугольника вокруг своей оси на 180 ° образуется прямой круговой конус.

4. В месте пересечения конуса плоскостью, параллельной основанию конуса, образуется круг. (см. Срезанный конус)

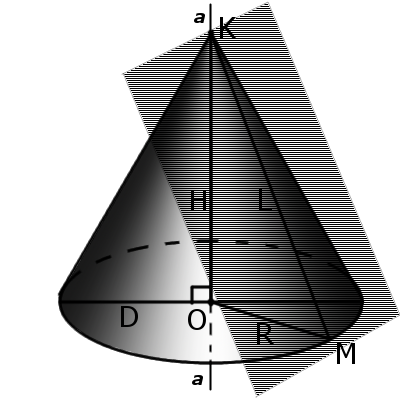
5. Если при пересечении плоскость не параллельна основе конуса и не пересекается с основанием, то в месте пересечения образуется эллипс (рис. 3).

6. Если плоскость сечения проходит через основание, то в месте пересечения образуется парабола (рис. 4).

7. Если плоскость сечения проходит через вершину, то в месте пересечения образуется равнобедренный треугольник (см. Осевое сечение).

8. Центр тяжести любого конуса находится на одной четвертой высоты от центра основы.

Формулы по геометрии Треугольник. Формулы и свойства треугольника

Квадрат. Формулы и свойства квадрата

Прямоугольник. Формулы и свойства прямоугольника

Параллелограмм. Формулы и свойства параллелограмма

Ромб. Формулы и свойства ромба

Трапеция. Формулы и свойства трапеции

- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции

- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции

Правильный многоугольник. Формулы и свойства правильного многоугольника

Окружность, круг, сегмент, сектор. Формулы и свойства

Эллипс. Формулы и свойства эллипса

Куб. Формулы и свойства куба

Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда Призма. Формулы и свойства призмы

Пирамида. Формулы и свойства пирамиды

Сфера, шар, сегмент и сектор. Формулы и свойства

Цилиндр. Формулы и свойства

Конус. Формулы и свойства

Формулы площади геометрических фигур S Формулы периметра геометрических фигур P Формулы объема геометрических фигур V Формулы площади поверхности геометрических фигур S

Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!