Эллипс. Формулы, признаки и свойства эллипсa
Навигация по странице:
Определение эллипсa
Элементы эллипсa
Основные свойства эллипсa
Уравнение эллипсa
Радиус круга вписанного в эллипс
Радиус круга описанного вокруг эллипса
Площадь эллипсa
Площадь сегмента эллипсa
Приближённая формула периметра эллипсa
Длина дуги эллипсa
Определение эллипсa
Определение.
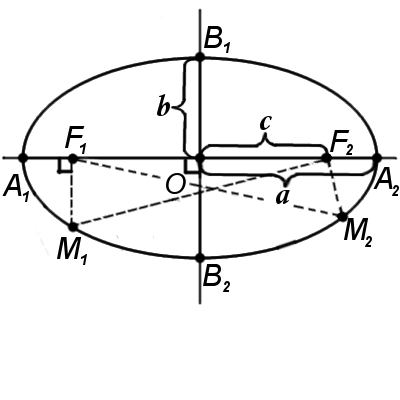
Эллипс — это замкнутая плоская кривая, сумма расстояний от каждой точки которой до двух точек F1 и F2 равна постоянной величине. Точки F1 и F2 называют фокусами эллипса.
F1M1 + F2M1 = F1M2 + F2M2 = A1A2 = const
 |
 |
|
| Рис.1 | Рис.2 |
Элементы эллипсa
F1 и F2 - фокусы эллипсa
Оси эллипсa.
А1А2 = 2a - большая ось эллипса (проходит через фокусы эллипса)
B1B2 = 2b - малая ось эллипса (перпендикулярна большей оси эллипса и проходит через ее центр)
a - большая полуось эллипса
b - малая полуось эллипса
O - центр эллипса (точка пересечения большей и малой осей эллипса)
Вершины эллипсa A1, A2, B1, B2 - точки пересечения эллипсa с малой и большой осями эллипсa
Диаметр эллипсa - отрезок, соединяющий две точки эллипса и проходящий через его центр.
Фокальное расстояние c - половина длины отрезка, соединяющего фокусы эллипсa.
Эксцентриситет эллипсa e характеризует его растяженность и определяется отношением фокального расстояния c к большой полуоси a. Для эллипсa эксцентриситет всегда будет 0 < e < 1, для круга e = 0, для параболы e = 1, для гиперболы e > 1.
| e = | c |
| a |
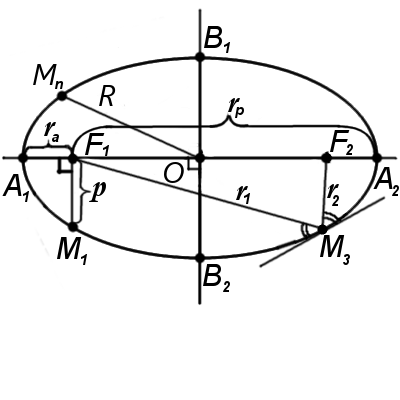
Фокальные радиусы эллипсa r1, r2 - расстояния от точки на эллипсе до фокусов.
Радиус эллипсa R - отрезок, соединяющий центр эллипсa О с точкой на эллипсе.
где e - эксцентриситет эллипсa, φ - угол между радиусом и большой осью A1A2.
| R = | ab | = | b |
| √a2sin2φ + b2cos2φ | √1 - e2cos2φ |
где e - эксцентриситет эллипсa, φ - угол между радиусом и большой осью A1A2.
Фокальный параметр эллипсa p - отрезок который выходит из фокуса эллипсa и перпендикулярный большой полуоси:
| p = | b2 |
| a |
Коэффициент сжатия эллипсa (эллиптичность) k - отношение длины малой полуоси к большой полуоси. Так как малая полуось эллипсa всегда меньше большей, то k < 1, для круга k = 1:
где e - эксцентриситет.
| k = | b |
| a |
k = √1 - e2
где e - эксцентриситет.
Сжатие эллипсa (1 - k ) - величина, которая равная разности между единицей и эллиптичностью:
| 1 - k = | a - b |
| a |
Директрисы эллипсa - две прямые перпендикулярные фокальной оси эллипса, и пересекающие ее на расстоянии a e p e
Основные свойства эллипсa
1. Угол между касательной к эллипсу и фокальным радиусом r1 равен углу между касательной и фокальным радиусом r2 (Рис. 2, точка М3).
2. Уравнение касательной к эллипсу в точке М с координатами (xM, yM):
| 1 = | xxM | + | yyM |
| a2 | b2 |
3. Если эллипс пересекается двумя параллельными прямыми, то отрезок, соединяющий середины отрезков образовавшихся при пересечении прямых и эллипса, всегда будет проходить через центр эллипсa. (Это свойство дает возможность построением с помощью циркуля и линейки получить центр эллипса.)
4. Эволютой эллипсa есть астероида, что растянута вдоль короткой оси.
5. Если вписать эллипс с фокусами F1 и F2 у треугольник ∆ ABC, то будет выполнятся следующее соотношение:
| 1 = | F1A ∙ F2A | + | F1B ∙ F2B | + | F1C ∙ F2C |
| CA ∙ AB | AB ∙ BC | BC ∙ CA |
Уравнение эллипсa
Каноническое уравнение эллипсa:
Уравнение описывает эллипс в декартовой системе координат. Если центр эллипсa О в начале системы координат, а большая ось лежит на абсциссе, то эллипсa описывается уравнением:
Если центр эллипсa О смещен в точку с координатами (xo, yo), то уравнение:
| 1 = | x2 | + | y2 |
| a2 | b2 |
| 1 = | (x - xo)2 | + | (y - yo)2 |
| a2 | b2 |
Параметрическое уравнение эллипсa:
| { | x = a cos α | де 0 ≤ α < 2π |
| y = b sin α |
Радиус круга вписанного в эллипс
Круг, вписан в эллипс касается только двух вершин эллипсa B1 и B2. Соответственно, радиус вписанного круга r будет равен длине малой полуоси эллипсa OB1:
r = b
Радиус круга описанного вокруг эллипсa
Круг, описан вокруг эллипсa касается только двух вершин эллипсa A1 и A2. Соответственно, радиус описанного круга R будет равен длине большой полуоси эллипсa OA1:
R = a
Площадь эллипсa
Формула определение площади эллипсa:
S = πab
Площадь сегмента эллипсa
Формула площади сегмента, что находится по левую сторону от хорды с координатами (x, y) и (x, -y):
| S = | πab | - | b | ( | x | √ | a2 - x2 + a2 ∙ arcsin | x | ) |
| 2 | a | a |
Периметр эллипсa
Найти точную формулу периметра эллипсa L очень тяжело. Ниже приведена формула приблизительной длины периметра. Максимальная погрешность этой формулы ~0,63 %:
| L ≈ 4 | πab + (a - b)2 |
| a + b |
Длина дуги эллипсa
Формулы определения длины дуги эллипсa:
1. Параметрическая формула определения длины дуги эллипсa через большую a и малую b полуоси:
| t2 | ||
| l = | ∫ | √a2sin2t + b2cos2t dt |
| t1 |
2. Параметрическая формула определения длины дуги эллипсa через большую полуось a и эксцентриситет e:
| t2 | ||
| l = | ∫ | √1 - e2cos2t dt, e < 1 |
| t1 |
Формулы по геометрии
Треугольник. Формулы и свойства треугольника  Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
 Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
