OnlineMSchool
Изучение математики онлайн.
Изучайте математику с нами и убедитесь: "Математика - это просто!"
Регистрация Войти Выйти

Правильный многоугольник. Формулы, признаки и свойства правильного многоугольника

Навигация по странице: Определение правильного многоугольника Признаки правильного многоугольника Основные свойства правильного многоугольника Правильный n-угольник - формулы       - длина стороны       - радиус вписанной окружности       - радиус описанной окружности       - площадь       - периметр       - угол между сторонами Правильный треугольник Правильный четырехугольник Правильный шестиугольник Правильный восьмиугольник
Определение. Правильный многоугольник — это многоугольник, у которого все стороны и углы одинаковые.
Многоугольником называется часть площади, которая ограничена замкнутой ломаной линией, не пересекающей сама себя.
Многоугольники отличаются между собой количеством сторон и углов.
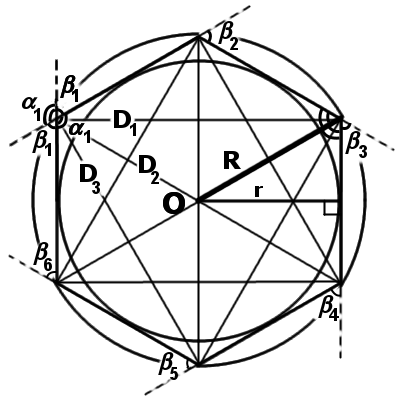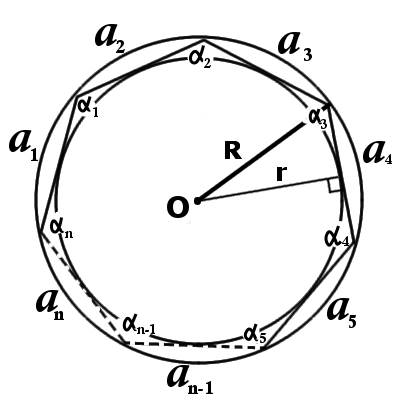Изображение правильного многоугольника с обозначениями Изображение правильного многоугольника с обозначениями
Рис.1 Рис.2

Признаки правильного многоугольника

Многоугольник будет правильным, если выполняется следующее условие:
Все стороны и углы одинаковы:

a1 = a2 = a3 = ... = an-1 = an

α1 = α2 = α3 = ... = αn-1 = αn


Основные свойства правильного многоугольника

1. Все стороны равны:
a1 = a2 = a3 = ... = an-1 = an
2. Все углы равны:
α1 = α2 = α3 = ... = αn-1 = αn
3. Центр вписанной окружности Oв совпадает з центром описанной окружности Oо, что и образуют центр многоугольника O
4. Сумма всех углов n-угольника равна:

180° · (n - 2)

5. Сумма всех внешних углов n-угольника равна 360°:

β1 + β2 + β3 + ... + βn-1 + βn = 360°

6. Количество диагоналей (Dn) n-угольника равна половине произведения количества вершин на количество диагоналей, выходящих из каждой вершины:
Dn = n · (n - 3)
2
7. В любой многоугольник можно вписать окружность и описать круг при этом площадь кольца, образованная этими окружностями, зависит только от длины стороны многоугольника:
S = πa2
4
8. Все биссектрисы углов между сторонами равны и проходят через центр правильного многоугольника O

Правильный n-угольник - формулы

Формулы длины стороны правильного n-угольника

1. Формула стороны правильного n-угольника через радиус вписанной окружности:
a = 2r · tg 180°
n
a = 2r · tgπ
n
2. Формула стороны правильного n-угольника через радиус описанной окружности:
a = 2 R · sin 180°
n
a = 2 R · sinπ
n

Формула радиуса вписанной окружности правильного n-угольника

Формула радиуса вписанной окружности n-угольника через длину стороны:
r = a : (2tg 180°)
n
r = a : (2tg π)
n

Формула радиуса описанной окружности правильного n-угольника

Формула радиуса описанной окружности n-угольника через длину стороны:
R = a : (2sin 180°)
n
R = a : (2sin π)
n

Формулы площади правильного n-угольника

1. Формула площади n-угольника через длину стороны:
S = na2 · ctg180°
4n
2. Формула площади n-угольника через радиус вписанной окружности:
S = nr2 · tg180°
n
3. Формула площади n-угольника через радиус описанной окружности:
S = nR2 · sin360°
2n

Формула периметра правильного многоугольника:

Формула периметра правильного n-угольника:

P = na

Формула определения угла между сторонами правильного многоугольника:

Формула угла между сторонами правильного n-угольника:
αn = n - 2 · 180°
n

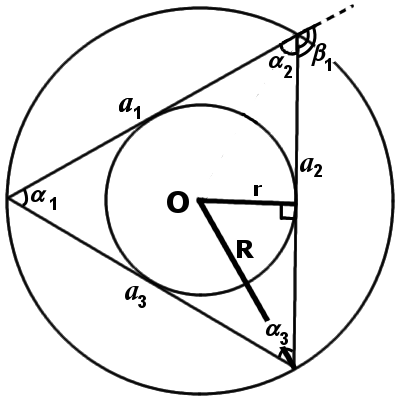Изображение правильного треугольника с обозначениями
Рис.3

Правильный треугольник

Формулы правильного треугольника:

1. Формула стороны правильного треугольника через радиус вписанной окружности:

a = 2r √3

2. Формула стороны правильного треугольника через радиус описанной окружности:

a = R√3

3. Формула радиуса вписанной окружности правильного треугольника через длину стороны:
r = a√3
6
4. Формула радиуса описанной окружности правильного треугольника через длину стороны:
R = a√3
3
5. Формула площади правильного треугольника через длину стороны:
S = a2√3
4
6. Формула площади правильного треугольника через радиус вписанной окружности:

S = r2 3√3

7. Формула площади правильного треугольника через радиус описанной окружности:
S = R2 3√3
4
8. Угол между сторонами правильного треугольника:

α = 60°


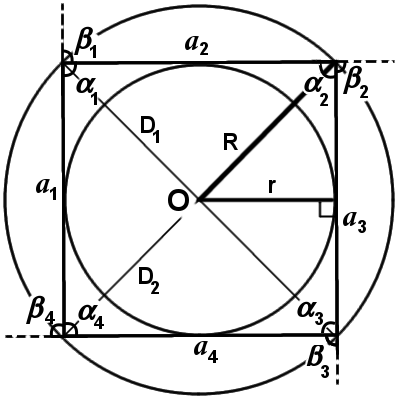Изображение правильного четырехугольнику с обозначениями
Рис.4

Правильный четырехугольник

Правильный четырехугольнику - квадрат.

Формулы правильного четырехугольника:

1. Формула стороны правильного четырехугольника через радиус вписанной окружности:

a = 2r

2. Формула стороны правильного четырехугольника через радиус описанной окружности:

a = R√2

3. Формула радиуса вписанной окружности правильного четырехугольника через длину стороны:
r = a
2
4. Формула радиуса описанной окружности правильного четырехугольника через длину стороны:
R = a√2
2
5. Формула площади правильного четырехугольника через длину стороны:

S = a2

6. Формула площади правильного четырехугольника через радиус вписанной окружности:

S = 4 r2

7. Формула площади правильного четырехугольника через радиус описанной окружности:

S =  2 R2

8. Угол между сторонами правильного четырехугольника:

α = 90°

Смотрите также формулы и свойства квадрата

Правильный шестиугольник

Формулы правильного шестиугольника:

1. Формула стороны правильного шестиугольника через радиус вписанной окружности:
a = 2√3r
3
2. Формула стороны правильного шестиугольника через радиус описанной окружности:

a = R

3. Формула радиуса вписанной окружности правильного шестиугольника через длину стороны:
r = a√3
2
4. Формула радиуса описанной окружности правильного шестиугольника через длину стороны:

R = a

5. Формула площади правильного шестиугольника через длину стороны:
S = a2 3√3
2
6. Формула площади правильного шестиугольника через радиус вписанной окружности:

S = r2 2√3

7. Формула площади правильного шестиугольника через радиус описанной окружности:
S = R2 3√3
2
8. Угол между сторонами правильного шестиугольника:

α = 120°


Правильный восьмиугольник

Формулы правильного восьмиугольника:

1. Формула стороны правильного восьмиугольника через радиус вписанной окружности:

a = 2r · (√2 - 1)

2. Формула стороны правильного восьмиугольника через радиус описанной окружности:

a = R√2 - √2

3. Формула радиуса вписанной окружности правильного восьмиугольника через длину стороны:
r = a(√2 + 1)
2
4. Формула радиуса описанной окружности правильного восьмиугольника через длину стороны:
R = a√4 + 2√2
2
5. Формула площади правильного восьмиугольника через длину стороны:

S = a2 2(√2 + 1)

6. Формула площади правильного восьмиугольника через радиус вписанной окружности:

S = r2 8(√2 - 1)

7. Формула площади правильного восьмиугольника через радиус описанной окружности:

S = R2 2√2

8. Угол между сторонами правильного восьмиугольника:

α = 135°

Формулы по геометрии Треугольник. Формулы и свойства треугольника Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Правильный многоугольник. Формулы и свойства правильного многоугольника Окружность, круг, сегмент, сектор. Формулы и свойства Эллипс. Формулы и свойства эллипса Куб. Формулы и свойства куба Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда Призма. Формулы и свойства призмы Пирамида. Формулы и свойства пирамиды Сфера, шар, сегмент и сектор. Формулы и свойства Цилиндр. Формулы и свойства Конус. Формулы и свойства Формулы площади геометрических фигур S Формулы периметра геометрических фигур P Формулы объема геометрических фигур V Формулы площади поверхности геометрических фигур S
Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0
Присоединяйтесь