OnlineMSchool
Изучение математики онлайн.
Изучайте математику с нами и убедитесь: "Математика - это просто!"
Регистрация Войти Выйти

Прямоугольник. Формулы и свойства прямоугольника

Навигация по странице: Определение прямоугольника Основные свойства прямоугольника Стороны прямоугольника (длина и ширина прямоугольника) Диагональ прямоугольника Периметр прямоугольника Площадь прямоугольника Окружность описанная вокруг прямоугольника Угол между стороной и диагональю прямоугольника Угол между диагоналями прямоугольника
Определение.
Прямоугольник - это четырехугольник у которого две противоположные стороны равны и все четыре угла одинаковы.

Прямоугольники отличаются между собой только отношением длинной стороны к короткой, но все четыре угла у них прямые, то есть по 90 градусов.

Длинную сторону прямоугольника называют длиной прямоугольника, а короткую - шириной прямоугольника.

Стороны прямоугольника одновременно является его высотами.

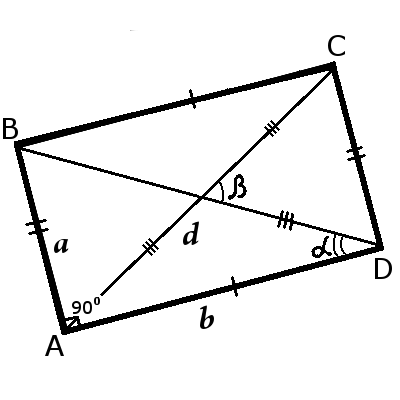
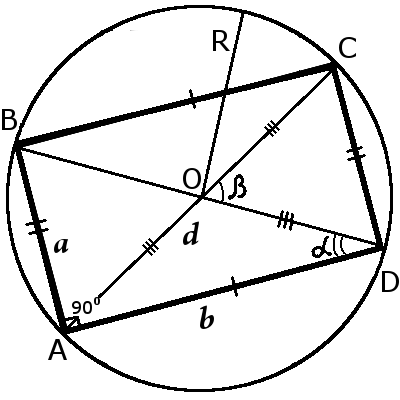
Изображение прямоугольника с обозначениями Изображение прямоугольника с обозначениями
Рис.1 Рис.2

Основные свойства прямоугольника

Прямоугольником могут быть параллелограмм, квадрат или ромб.
1. Противоположные стороны прямоугольника имеют одинаковую длину, то есть они равны:

AB = CD,   BC = AD

2. Противоположные стороны прямоугольника параллельны:

AB||CD,   BC||AD

3. Прилегающие стороны прямоугольника всегда перпендикулярны:

AB ┴ BC,   BC ┴ CD,   CD ┴ AD,   AD ┴ AB

4. Все четыре угла прямоугольника прямые:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

5. Сумма углов прямоугольника равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

6. Диагонали прямоугольника имеют одинаковой длины:

AC = BD

7. Сумма квадратов диагонали прямоугольника равны сумме квадратов сторон:

2d2 = 2a2 + 2b2

8. Каждая диагональ прямоугольника делит прямоугольник на две одинаковые фигуры, а именно на прямоугольные треугольники.
9. Диагонали прямоугольника пересекаются и в точке пересечения делятся пополам:

         AO = BO = CO = DO =  d
2
10. Точка пересечения диагоналей называется центром прямоугольника и также является центром описанной окружности
11. Диагональ прямоугольника является диаметром описанной окружности
12. Вокруг прямоугольника всегда можно описать окружность, так как сумма противоположных углов равна 180 градусов:

∠ABC + ∠CDA = 180°   ∠BCD + ∠DAB = 180°

13. В прямоугольник, у которого длина не равна ширине, нельзя вписать окружность, так как суммы противоположных сторон не равны между собой (вписать окружность можно только в частный случай прямоугольника - квадрат).

Стороны прямоугольника

Определение.
Длиной прямоугольника называют длину более длинной пары его сторон. Шириной прямоугольника называют длину более короткой пары его сторон.

Формулы определения длин сторон прямоугольника

1. Формула стороны прямоугольника (длины и ширины прямоугольника) через диагональ и другую сторону:

a = √d2 - b2

b = √d2 - a2

2. Формула стороны прямоугольника (длины и ширины прямоугольника) через площадь и другую сторону:
a = S
b
b = S
a
3. Формула стороны прямоугольника (длины и ширины прямоугольника) через периметр и другую сторону:
a = P - 2b
2
b = P - 2a
2
4. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол α:

a = d sinα

b = d cosα

5. Формула стороны прямоугольника (длины и ширины прямоугольника) через диаметр и угол β:
a = d sin β
2
b = d cos β
2

Диагональ прямоугольника

Определение.
Диагональю прямоугольника называется любой отрезок соединяющий две вершины противоположных углов прямоугольника.

Формулы определения длины диагонали прямоугольника

1. Формула диагонали прямоугольника через две стороны прямоугольника (через теорему Пифагора):

d = √a2 + b2

2. Формула диагонали прямоугольника через площадь и любую сторону:
d = √S2 + a4 = √S2 + b4
ab
3. Формула диагонали прямоугольника через периметр и любую сторону:
d = √P2 - 4Pa + 8a2 = √P2 - 4Pb + 8b2
22
4. Формула диагонали прямоугольника через радиус описанной окружности:

d = 2R

5. Формула диагонали прямоугольника через диаметр описанной окружности:

d = Dо

6. Формула диагонали прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
d = a
sin α
7. Формула диагонали прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
d = b
cos α
8. Формула диагонали прямоугольника через синус острого угла между диагоналями и площадью прямоугольника

d = √2S : sin β


Периметр прямоугольника

Определение.
Периметром прямоугольника называется сумма длин всех сторон прямоугольника.

Формулы определения длины периметру прямоугольника

1. Формула периметру прямоугольника через две стороны прямоугольника:

P = 2a + 2b

P = 2(a + b)

2. Формула периметру прямоугольника через площадь и любую сторону:
P = 2S + 2a2 = 2S + 2b2
ab
3. Формула периметру прямоугольника через диагональ и любую сторону:

P = 2(a + √d2 - a2) = 2(b + √d2 - b2)

4. Формула периметру прямоугольника через радиус описанной окружности и любую сторону:

P = 2(a + √4R2 - a2) = 2(b + √4R2 - b2)

5. Формула периметру прямоугольника через диаметр описанной окружности и любую сторону:

P = 2(a + √Do2 - a2) = 2(b + √Do2 - b2)


Площадь прямоугольника

Определение.
Площадью прямоугольника называется пространство ограниченный сторонами прямоугольника, то есть в пределах периметра прямоугольника.

Формулы определения площади прямоугольника

1. Формула площади прямоугольника через две стороны:

S = a · b

2. Формула площади прямоугольника через периметр и любую сторону:
S = Pa - 2a2 = Pb - 2b2
22
3. Формула площади прямоугольника через диагональ и любую сторону:

S = a√d2 - a2 = b√d2 - b2

4. Формула площади прямоугольника через диагональ и синус острого угла между диагоналями:
S = d2 · sin β
2
5. Формула площади прямоугольника через радиус описанной окружности и любую сторону:

S = a√4R2 - a2 = b√4R2 - b2

6. Формула площади прямоугольника через диаметр описанной окружности и любую сторону:

S = a√Do2 - a2 = b√Do2 - b2


Окружность описанная вокруг прямоугольника

Определение.
Окружностью описанной вокруг прямоугольника называется круг проходящий через четыре вершины прямоугольника, центр которого лежит на пересечении диагоналей прямоугольника.

Формулы определения радиуса окружности описанной вокруг прямоугольника

1. Формула радиуса окружности описанной вокруг прямоугольника через две стороны:
R = √a2 + b2
2
2. Формула радиуса окружности описанной вокруг прямоугольника через периметр квадрата и любую сторону:
R = √P2 - 4Pa + 8a2 = √P2 - 4Pb + 8b2
44
3. Формула радиуса окружности описанной вокруг прямоугольника через площадь квадрата:
R = √S2 + a4 = √S2 + b4
2a2b
4. Формула радиуса окружности описанной вокруг прямоугольника через диагональ квадрата:
R = d
2
5. Формула радиуса окружности описанной вокруг прямоугольника через диаметр описанной окружности:
R = Dо
2
6. Формула радиуса окружности описанной вокруг прямоугольника через синус угла, прилегающего к диагонали, и длину стороны противоположной этому углу:
R = a
2sin α
7. Формула радиуса окружности описанной вокруг прямоугольника через косинус угла, прилегающего к диагонали, и длину стороны прилегающей к этому углу:
R = b
2cos α
8. Формула радиуса окружности описанной вокруг прямоугольника через синус острого угла между диагоналями и площадью прямоугольника:
R = √2S : sin β
2

Угол между стороной и диагональю прямоугольника

Формулы определения угла между стороной и диагональю

1. Формула определения угла между стороной и диагональю прямоугольника через диагональ и сторону:
sin α = a
d
cos α = b
d
2. Формула определения угла между стороной и диагональю прямоугольника через угол между диагоналями:
α = β
2

Угол между диагоналями прямоугольника

Формулы определения угла между диагоналями прямоугольника

1. Формула определения угла между диагоналями прямоугольника через угол между стороной и диагональю:

β = 2α

2. Формула определения угла между диагоналями прямоугольника через площадь и диагональ:
sin β = 2S
d2
Формулы по геометрии Треугольник. Формулы и свойства треугольника Квадрат. Формулы и свойства квадрата Прямоугольник. Формулы и свойства прямоугольника Параллелограмм. Формулы и свойства параллелограмма Ромб. Формулы и свойства ромба Трапеция. Формулы и свойства трапеции - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции Правильный многоугольник. Формулы и свойства правильного многоугольника Окружность, круг, сегмент, сектор. Формулы и свойства Эллипс. Формулы и свойства эллипса Куб. Формулы и свойства куба Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда Призма. Формулы и свойства призмы Пирамида. Формулы и свойства пирамиды Сфера, шар, сегмент и сектор. Формулы и свойства Цилиндр. Формулы и свойства Конус. Формулы и свойства Формулы площади геометрических фигур S Формулы периметра геометрических фигур P Формулы объема геометрических фигур V Формулы площади поверхности геометрических фигур S
Все таблицы и формулы

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

0
Присоединяйтесь