Формулы площади геометрических фигур
Площадь геометрической фигуры - численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади плоских фигур:
 Формулы площади треугольника
Формулы площади треугольника
 Формулы площади квадрата
Формулы площади квадрата
 Формула площади прямоугольника
Формула площади прямоугольника
 Формулы площади параллелограмма
Формулы площади параллелограмма
 Формулы площади ромба
Формулы площади ромба
 Формула площади трапеции
Формула площади трапеции
 Формула площади выпуклого четырехугольника
Формула площади выпуклого четырехугольника
 Формулы площади круга
Формулы площади круга
 Формулы площади эллипса
Формулы площади эллипса
 Формулы площади треугольника
Формулы площади треугольника
 Формулы площади квадрата
Формулы площади квадрата
 Формула площади прямоугольника
Формула площади прямоугольника
 Формулы площади параллелограмма
Формулы площади параллелограмма
 Формулы площади ромба
Формулы площади ромба
 Формула площади трапеции
Формула площади трапеции
 Формула площади выпуклого четырехугольника
Формула площади выпуклого четырехугольника
 Формулы площади круга
Формулы площади круга
 Формулы площади эллипса
Формулы площади эллипса
Формулы площади треугольника

- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высотыS = 1 a · h 2 - Формула площади треугольника по трем сторонам
Формула Герона
S = √p(p - a)(p - b)(p - c) - Формула площади треугольника по двум сторонам и углу между ними
Площадь треугольника равна половине произведения двух его сторон умноженного на синус угла между ними.S = 1 a · b · sin γ 2 S = 1 a · c · sin β 2 S = 1 b · c · sin α 2 - Формула площади треугольника по трем сторонам и радиусу описанной окружности
S = a · b · с 4R - Формула площади треугольника по трем сторонам и радиусу вписанной окружностигде S - площадь треугольника,
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности.S = p · r
a, b, c - длины сторон треугольника,
h - высота треугольника,
γ - угол между сторонами a и b,
r - радиус вписанной окружности,
R - радиус описанной окружности,
p = a + b + c - полупериметр треугольника. 2
Формулы площади квадрата

- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны.
S = a2 - Формула площади квадрата по длине диагоналигде S - площадь квадрата,
Площадь квадрата равна половине квадрата длины его диагонали.S = 1 d2 2
a - длина стороны квадрата,
d - длина диагонали квадрата.
Формула площади прямоугольника

Площадь прямоугольника равна произведению длин двух его смежных сторон
где S - Площадь прямоугольника,S = a · b
a, b - длины сторон прямоугольника.
Формулы площади параллелограмма

- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
S = a · b · sin α - Формула площади параллелограмма по двум диагоналям и углу между нимигде S - Площадь параллелограмма,
Площадь параллелограмма равна половине произведения длин его диагоналей умноженному на синус угла между ними.
S = 1 d1d2 sin γ 2
a, b - длины сторон параллелограмма,
h - длина высоты параллелограмма,
d1, d2 - длины диагоналей параллелограмма,
α - угол между сторонами параллелограмма,
γ - угол между диагоналями параллелограмма.
Формулы площади ромба

- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.
S = a · h - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.
S = a2 · sin α - Формула площади ромба по длинам его диагоналейгде S - Площадь ромба,
Площадь ромба равна половине произведению длин его диагоналей.
S = 1 d1 · d2 2
a - длина стороны ромба,
h - длина высоты ромба,
α - угол между сторонами ромба,
d1, d2 - длины диагоналей.
Формулы площади трапеции

- Формула Герона для трапеции
S = a + b √(p-a)(p-b)(p-a-c)(p-a-d) |a - b| - Формула площади трапеции по длине основ и высотегде S - площадь трапеции,
Площадь трапеции равна произведению полусуммы ее оснований на высоту
S = 1 (a + b) · h 2
a, b - длины основ трапеции,
c, d - длины боковых сторон трапеции,
p = a + b + c + d - полупериметр трапеции. 2
Формулы площади выпуклого четырехугольника

- Формула площади четырехугольника по длине диагоналей и углу между нимигде S - площадь четырехугольника,
Площадь выпуклого четырехугольника равна половине произведения его диагоналей умноженному на синус угла между ними:
S = 1 d1 d2 sin α 2
d1, d2 - длины диагоналей четырехугольника,
α - угол между диагоналями четырехугольника. - Формула площади описанного четырехугольника (по длине периметра и радиусу вписанной окружности)
Площадь выпуклого четырехугольника равна произведению полупериметра на радиус вписанной окружности
S = p · r  Формула площади четырехугольника по длине сторон и значению противоположных угловгде S - площадь четырехугольника,
Формула площади четырехугольника по длине сторон и значению противоположных угловгде S - площадь четырехугольника,
S = √(p - a)(p - b)(p - c)(p - d) - abcd cos2θa, b, c, d - длины сторон четырехугольника,
p =
a + b + c + d 2 θ =
α + β 2 -
Формула площади четырехугольника, вокруг которого можно описать окружность
S = √(p - a)(p - b)(p - c)(p - d)
Формулы площади круга

- Формула площади круга через радиус
Площадь круга равна произведению квадрата радиуса на число пи.
S = π r2 - Формула площади круга через диаметргде S - Площадь круга,
Площадь круга равна четверти произведения квадрата диаметра на число пи.S = 1 π d2 4
r - длина радиуса круга,
d - длина диаметра круга.
Формулы площади эллипса
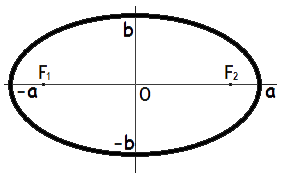
Площадь эллипса равна произведению длин большой и малой полуосей эллипса на число пи.
где S - Площадь эллипса,
S = π · a · b
a - длина большей полуоси эллипса,
b - длина меньшей полуоси эллипса.
Формулы по геометрии
Треугольник. Формулы и свойства треугольника  Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
 Квадрат. Формулы и свойства квадрата
Квадрат. Формулы и свойства квадрата  Прямоугольник. Формулы и свойства прямоугольника
Прямоугольник. Формулы и свойства прямоугольника  Параллелограмм. Формулы и свойства параллелограмма
Параллелограмм. Формулы и свойства параллелограмма  Ромб. Формулы и свойства ромба
Ромб. Формулы и свойства ромба  Трапеция. Формулы и свойства трапеции
Трапеция. Формулы и свойства трапеции  - Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции
- Равнобедренная трапеция. Формулы и свойства равнобедренной трапеции  - Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции
- Прямоугольная трапеция. Формулы и свойства прямоугольной трапеции  Правильный многоугольник. Формулы и свойства правильного многоугольника
Правильный многоугольник. Формулы и свойства правильного многоугольника  Окружность, круг, сегмент, сектор. Формулы и свойства
Окружность, круг, сегмент, сектор. Формулы и свойства  Эллипс. Формулы и свойства эллипса
Эллипс. Формулы и свойства эллипса  Куб. Формулы и свойства куба
Куб. Формулы и свойства куба  Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы
Прямоугольный параллелепипед. Формулы и свойства прямоугольного параллелепипеда
Призма. Формулы и свойства призмы  Пирамида. Формулы и свойства пирамиды
Пирамида. Формулы и свойства пирамиды  Сфера, шар, сегмент и сектор. Формулы и свойства
Сфера, шар, сегмент и сектор. Формулы и свойства  Цилиндр. Формулы и свойства
Цилиндр. Формулы и свойства  Конус. Формулы и свойства
Конус. Формулы и свойства  Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Формулы площади геометрических фигур S
Формулы периметра геометрических фигур P
Формулы объема геометрических фигур V
Формулы площади поверхности геометрических фигур S
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

